Предмет: Геометрия,
автор: mmsafonov
Вершина параллелограмма равноудалена
от середин двух его сторон. Докажите, что
этот параллелограмм – ромб
Ответы
Автор ответа:
15
Если вершина A равноудалена от середин сторон AB и AD, то очевидно: половины смежных сторон равны => смежные стороны равны => параллелограмм с равными смежными сторонами - ромб.
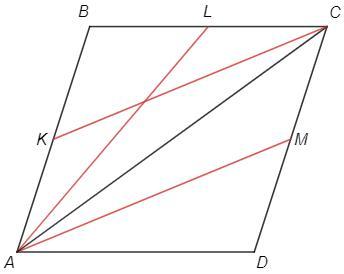
L - середина BC, M - середина CD, AL=AM.
Пусть K - середина AB, тогда AKCM - параллелограмм (т.к. AK=CM, AK||CM).
AL=AM=CK
В треугольнике ABC медианы равны - треугольник равнобедренный, AB=BC.
Параллелограмм с равными смежными сторонами - ромб.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: ohip
Предмет: Русский язык,
автор: svetlanamiki
Предмет: Русский язык,
автор: polechkaluna
Предмет: Математика,
автор: Кристина2086
Предмет: География,
автор: lerataranok010