Question

Діагональ паралелограма утворює з його сторонами кути 30°
і 90°. Знайдіть сторони паралелограма, якщо його периметр
дорівнює 36 см.​

Answer 1

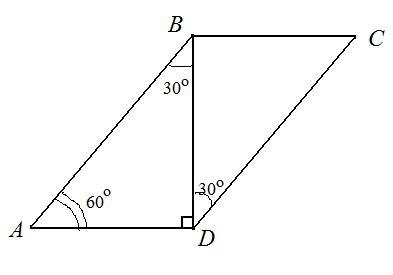
См. рисунок.

Пусть дан параллелограмм АВСD. ВD - диагональ, ∠АDВ = 90°,

∠ВDС = 30°, Р = 36 см. Найдем стороны параллелограмма.

∠АВС = ∠АDВ + ∠ВDС = 90° + 30° = 120°, тогда ∠ВАD = 180° - 120° = 60° (сумма углов параллелограмма, прилежащих к одной стороне, равна 180°).

Рассмотрим ΔАВD - прямоугольный. ∠АВD + ∠ВАD = 90° ( сумма острых углов прямоугольного треугольника равна 90°), значит,

∠АВD = 90° - 60° = 30°.

По свйству катета, лежащего против угла в 30°, он равен половине гипотенузы, т.е. АВ = 2АD.

У параллелограмма противоположные стороны равны, т.е. АВ = СD, АD = ВС, т.е. Р = 2(АВ + АD) = 36 см, откуда АВ + АD = 36 : 2 = 18 (см).

Т.к. АВ = 2АD, то 2АD + АD = 18, 3АD = 18, откуда АD = 6 (см), тогда АВ = 2АD = 2 · 6 = 12 (см).

Таким образом, стороны параллелограмма равны:

АВ = СD = 12 см, ВС = АD = 6 см.

Ответ: 12 см, 6 см, 12 см и 6 см.

Answer 2

Ответ:

6, 6, 12 и 12 см

Объяснение:

По св-ву параллелограмма: AB=CD и AD=BC

Т. к. AC ⟂ CD => ∆ACD - п/у

$sin \: CAD = \frac{CD}{AD} \\ CD = AD \times sin \: 30^{\circ} \\ CD = 0.5 \times AD$

Теперь выразим сторону через периметр параллелограмма:

$P = 2(AD + CD) \\ \frac{P}{2} = AD + CD \\ \frac{P}{2} - AD= CD$

Теперь приравняем обе части:

$CD = 0.5 \times AD \\ CD = \frac{P}{2} - AD \\ \\ 0.5 \: AD= \frac{P}{2} - AD \: | \times 2 \\ AD = P - 2AD \\ 3AD = P \\ 3AD = 36 \\ AD = \frac{36}{3} = 12$

Теперь найдём другую сторону:

$CD = 0.5 \times 12 = 6$

Значит AB=CD = 6 см и AD=BC = 12 см