Предмет: Алгебра,
автор: ghhhiooi
Помогите,пожалуйста,срочно....
Приложения:
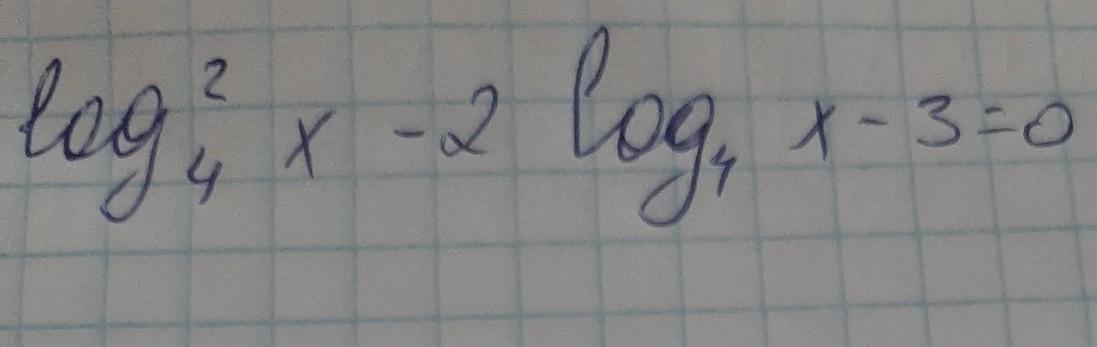
Ответы
Автор ответа:
0
ОДЗ : x > 0
ghhhiooi:
эмммм....ничего не понятноо(
Автор ответа:
0
Ответ:
Объяснение:
ОДЗ:
Решение:
Введём замену:
Перепишем исходное уравнение с учётом замены:
Вернёмся к замене:
Похожие вопросы
Предмет: Другие предметы,
автор: KotikSlava
Предмет: Русский язык,
автор: viktorijaanisi
Предмет: Другие предметы,
автор: Y2J2015
Предмет: Математика,
автор: марьянкова
Предмет: Математика,
автор: ник123096