Предмет: Геометрия,
автор: george423
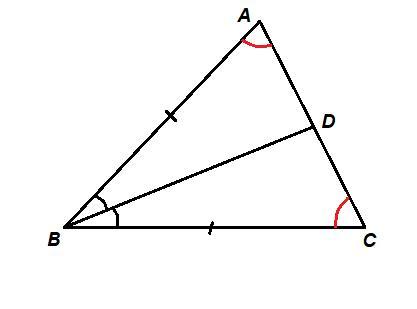
В треугольнике ABC проведена биссектриса BD. Докажите что треугольники ABD и CBD равны если AB=BC угол A равен углу C
20 баллов
Ответы
Автор ответа:
0
Ответ:
Дано:
ΔАВС, BD - биссектриса,
АВ = ВС, ∠А = ∠С
Доказать:
ΔABD = ΔCBD
Доказательство:
В треугольниках ABD и CBD:
- АВ = ВС по условию,
- ∠АВD = ∠CBD, так как BD биссектриса,
- BD - общая сторона,
Значит, ΔABD = ΔCBD по двум сторонам и углу между ними.
Условие ∠А = ∠С при таком доказательстве лишнее.
Или можно иначе:
- АВ = ВС по условию,
- ∠АВD = ∠CBD, так как BD биссектриса,
- ∠А = ∠С по условию,
Значит, ΔABD = ΔCBD по стороне и двум прилежащим к ней углам.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: krasnova250148
Предмет: Русский язык,
автор: dimasic150703
Предмет: Другие предметы,
автор: dbelovitskaya
Предмет: Математика,
автор: Помагитеэтосрочна
Предмет: Математика,
автор: znanijacom1234