Пожалуйста, помогите с аналитической геометрией

Ответы
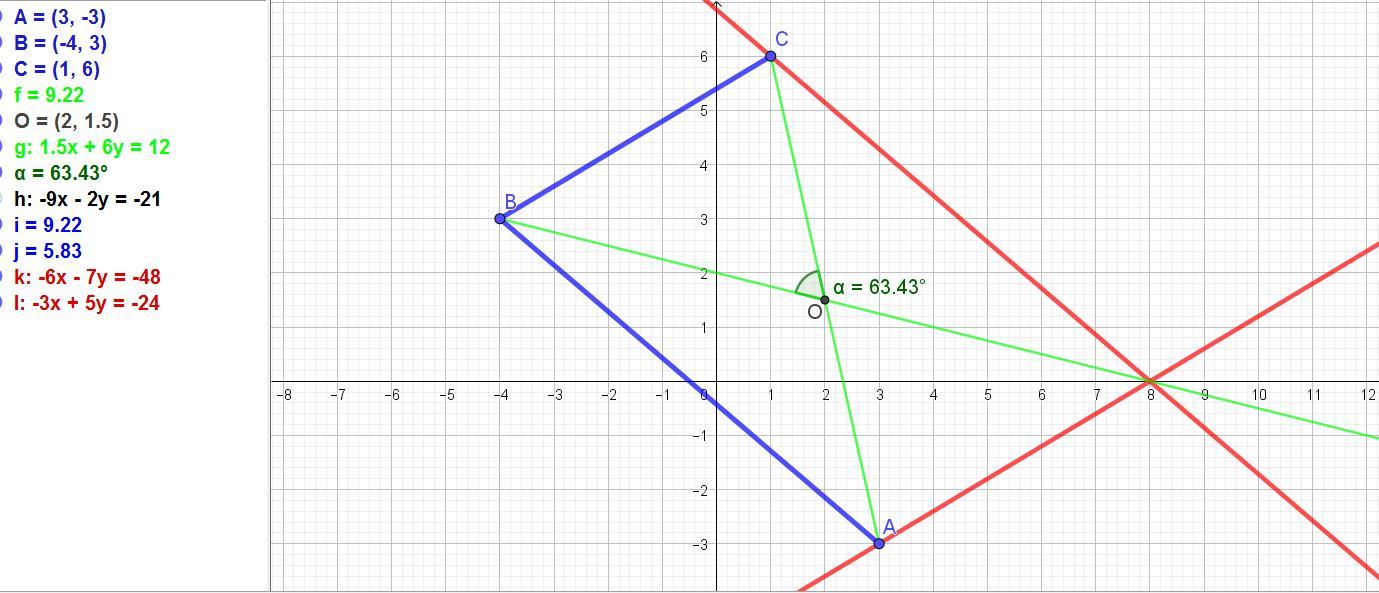
Даны три вершины: А(3; -3), В(-4; 3), С(1; 6).
1) Уравнение АD.
Так как прямая АД параллельна ВС, то её направляющий вектор сохраняется, как и у прямой ВС.
Вектор ВС: (1 - (-4); 6-3) = (5; 3).
Уравнение ВС: (x + 4)/5 = (y - 3)/3.
В общем виде: 3x - 5y + 27 = 0.
Подставив известные координаты точки А, получим уравнение АD.
Уравнение AD: (x - 3)/5 = (y + 3)/3.
В общем виде: 3x - 5y - 24 = 0.
2) Уравнение высоты ВК на сторону AD.
Прямая ВК перпендикулярна и АД и ВС.
У прямой, перпендикулярной к прямой ВС 3x - 5y + 27 = 0 в виде Ах + Ву + С = 0, коэффициенты А и В меняются на -В и А.
Уравнение ВК: 5х + 3у + С = 0.
Для определения слагаемого С подставим координаты известной точки В(-4; 3): 5*(-4) + 3*3 + С = 0, -20 + 9 + С = 0, С = 11.
Уравнение ВК: 5х + 3у + 11 = 0.
3) Длина высоты ВК.
Для вычисления расстояния от точки M(Mx; My) до прямой Ax + By + C = 0 используем формулу:
d = |A·Mx + B·My + C| /√(A² + B²).
Подставим в формулу данные:
d = |3·(-4) + (-5)·3 + (-24)|/ √(3² + (-5)²) = |-12 - 15 - 24|/ √(9 + 25) =
= 51/ √34 = 3√34/ 2 ≈ 8.7464278.
4) Уравнение диагонали BD.
Так как эта диагональ проходит через точку О (это точка пересечения диагоналей и середина АС), то уравнение можно составить по двум точкам: В и О.
Находим координаты точки О = АС/2 = (А(3; -3) + С(1; 6))/2 = (2; 1,5).
Вектор ВО = (2-(-4); 1,5-3)= (6; -1,5).
Уравнение ВО = ВД: (х + 4)/6 = (у - 3)/(-1,5) или в целых числах
(х + 4)/(-4) = (у - 3)/1. В общем виде х + 4у - 8 = 0.
5) Находим угловые коэффициенты прямых ВО и АО.
к(ВО) = -1,5/6 = -1/4 = -0,25.
к(АО) = (1,5-(-3))/(2-3) = 4,5/(-1) = -4,5.
угол между ними можно найти, используя формулу:
tg γ = k1 - k2
1 + k1·k2.
Подставим данные: у:
tg γ = -0,25 - (-4,5) = 2.
1 + (-0,25)*(-4,5)