Предмет: Алгебра,
автор: ovr1602
Помогите решить показательное уравнение
2*4,5^(x+1)-5*3^(x+1)+6*2^(x)=0
Приложения:
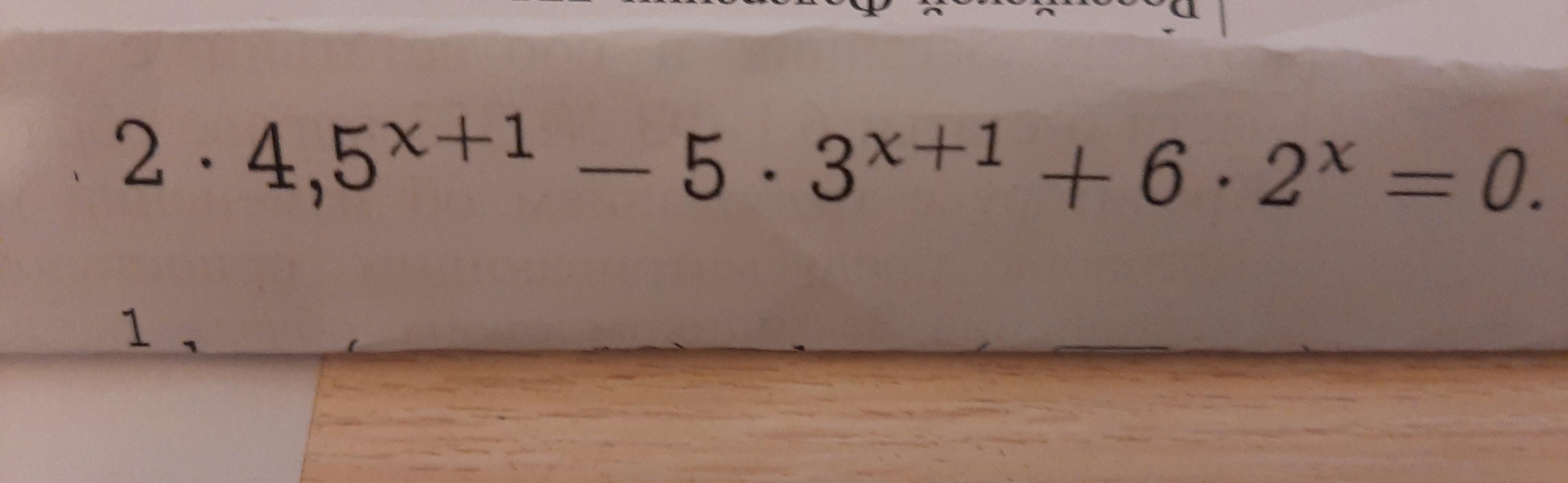
Ответы
Автор ответа:
2
Ответ:
X1 = 0
X2 = -1
Пошаговое решение:
2×(9/2)^x+1-5×3^x+1+6×2^x=0
2×9^x+1/2^x+1-5×3^x+1+6×2^x=0
9^x+1/2^x-5×3^x+1+6×2^x=0
9^x+1-5×2^x×3^x+1+6×2^2x/2^x=0
9^x+1-5×2×3^x+1+6×4^x/2^x-0
9^x+1-5×2^x×3^x+1+6×4^x=0
9^x+1-2×2^x×3^x+1-3×2^x×3^x+1+6×4^x=0
3^x+1×(3^x+1-2×2^x)-3×2^x×(3^x+1-2×2^x)=0
(3^x+1-3×2^x)×(3^x+1-2×2^x)=0
(3^x+1-3×2^x)×(3^x+1-2^x+1)=0
3^x+1-3×2^x=0
3^x+1-2^x+1=0
x=0
x=-1
X1 = -1
X2 = 0
Удачи!
Похожие вопросы
Предмет: Другие предметы,
автор: dimasik3082
Предмет: Русский язык,
автор: oksanaidima
Предмет: Русский язык,
автор: prusova81
Предмет: Алгебра,
автор: krokiki
Предмет: Химия,
автор: IdzayOrixara