Предмет: Алгебра,
автор: SilenceFlicking111
Ребята, объясните мне пожалуйста по какому принципу нужно решать это... (10 класс)
Приложения:
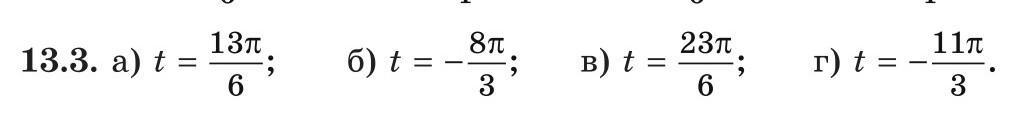
Universalka:
Какой вопрос к этому заданию ?
Нужно найти синус и косинус, не пойму по какому принципу
забыл написать
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Русский язык,
автор: terzivichka
Предмет: Русский язык,
автор: lizalove765
Предмет: Қазақ тiлi,
автор: gulruh1
Предмет: Математика,
автор: alina1427
Предмет: Музыка,
автор: UTASHINA