Дам 30 баллов.
1.Площадь прямоугольного треугольника равна 45 см2. Найдите его больший катет, если катеты относятся как 2:5.
2.Высота треугольника 5 дм , основание 12,7 дм. Найдите площадь этого треугольника
3.Найдите площадь прямоугольной трапеции, если её острый угол равен 45 градусам, а основания равны 7 м и 11 м.
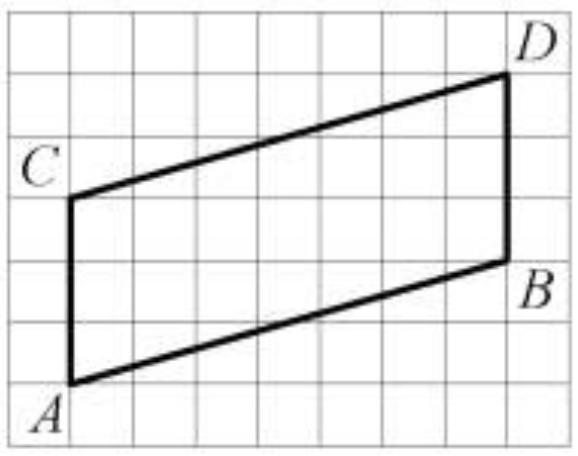
4.На клетчатой бумаге с размером клетки 1×1 изображен параллелограмм. Найдите его площадь. рис 1.
5.Смежные стороны параллелограмма равны 16,2 см и 14 см, а его острый угол равен 30 градусам. Найдите площадь параллелограмма.
6.Площадь ромба 24 см2. Длина одной из его диагоналей 8 см. Найдите длину другой диагонали
7.Длина диагонали квадрата равна 5 см. Найдите его площадь
8.Периметр прямоугольника 24 см, его длина относится к ширине как 3:1. Найдите площадь этого прямоугольника
9.В треугольнике АВС АВ = 14 см, ВС = 20 см, высота, проведенная к стороне АВ, равна 10 см. Найдите высоту, проведенную к стороне ВС
К заданию № 4
Ответы
Ответ:
1. 15 см.
2. 31,75 см².
3. 36 м².
4. 21 кв. ед.
5. 113,4 см².
6. 6 см.
7. 50 см².
8. 27 см².
9. 7 см.
Объяснение:
1. Пусть меньший катет равен 2х. Тогда больший равен 5х.
S=1/2(ah)=1/2(2x*5x)=(1/2)10x²=5x²;
5x²=45;
x²=9;
х=±3; (-3 - не соответствует условию) .
х=3 см.
Больший катет равен 5х=5*3=15 см.
***
Площадь треугольника вычисляется по формуле:
S=1/2 ah;
S=12.7*5/2= 31.75см².
***
3. ABCD - прямоугольная трапеция. ∠А=∠В=90°. ВС=7 м, AD=11 м.
∠D=45°. Высота СЕ отсекает равносторонний треугольник СЕD, у которого ∠D=45°, CE⊥AD.
ED=CE=AD-BC=11-7=4 м.
S=h(a+b)/2=4(7+11)/2=2*18=36 м².
***
4. Есть несколько способов вычисления площадей фигур на клетчатой бумаге. Предложу свой.
Дополним параллелограмм до прямоугольника и вычтем площади дополнительных треугольников (см. приложение).
S=S(прямоугольника) - 2S(треугольника);
S=5*7-2(2*7)/2=35-14= 21 кв. ед.
***
5. S=ah, где а=16,2 см. Найдем h.
BE/AB=Sin 30°;
BE=AB*Sin30° =14*(1/2)=7 см.
S=16.2*7=113.4 см²
***
6. Площадь ромба по его диагоналям:
S=D*d/2;
d=2S/D=2*24/8=48/8=6 см.
***
7. Пусть сторона квадрата равна а см.
Найдем а: 5²= а²+а²; 2а²=5²; а=√(5²)/2=5√2 см;
S=a²=(5√2)²=50 см².
***
8. Пусть одна сторона равна х тогда вторая равна 3х.
Р(ABCD)=2(AB+BC);
2(x+3x)=24;
4x=12;
x=3 см - меньшая сторона (AB).
Большая сторона равна 3х=3*3=9 см (BC).
Площадь равна S=AB*BC=3*9=27 см².
***
9. S(ABC)=(1/2)AB*CE=1/2*14*10=70 см².
Ту же площадь можно найти по формуле:
S=1/2(BC*AF), где AF - высота, проведенная к стороне ВС
1/2(20*AF)=70;
20*AF=140;
AF=140/20=7 см.