Question

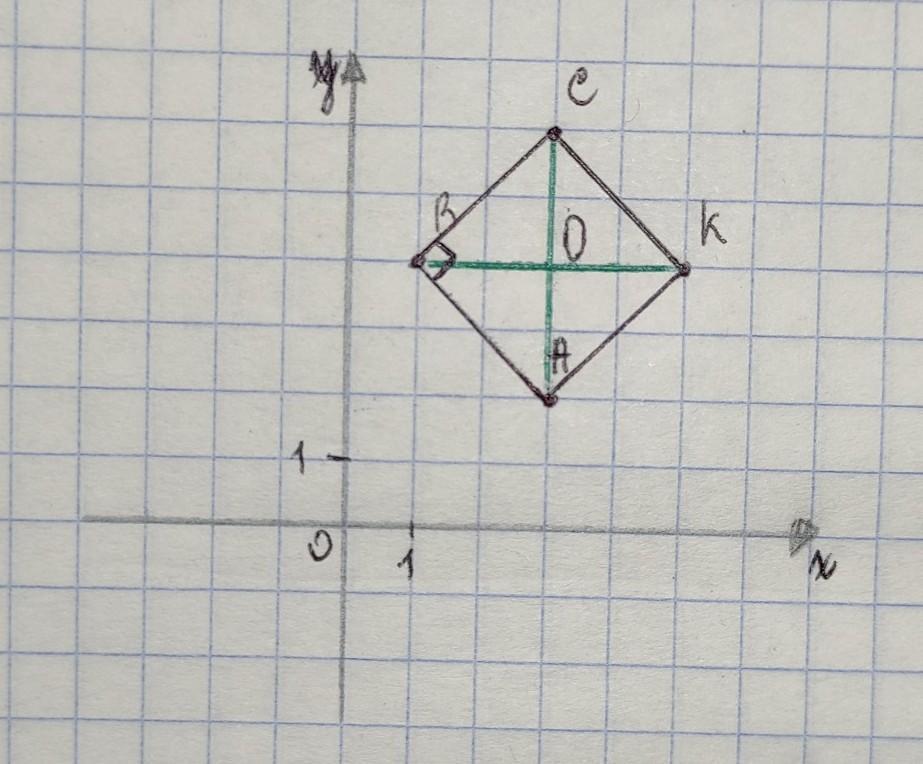
Впишите правильный ответ. Точка О – точка пересечения диагоналей квадрата АВСК. Найдите координату точки О и длину диагоналей, если вершины квадрата имеют следующие координаты: А (3; 2), В (1; 4), С (3; 6), К (5; 4). Ответ: О ( ; ), AC = , BK = . Сбросить ответы

Answer 1

Ответ:

O (3;4)

AC=BK = 4

Объяснение:

Раз ABCK - квадрат и т. O - т. пересечения диагоналей AC и BK => AO=OC по св-ву) => т. O - середина диагонали AC

$Xo = \frac{Xa +Xc}{2} = \frac{3 + 3}{2} = \frac{6}{2} = 3$

$Yo = \frac{Yo + Yc}{2} = \frac{2 + 6}{2} = \frac{8}{2} = 4$

Значит координаты т. O (3;4)

Чтобы найти длину отрезка, воспользуемся формулой:

$|ac| = \sqrt{ (Xc - Xa)^{2} + ( Yc - Ya)^{2} } \\ |AC| = \sqrt{(3 - 3)^{2} + (6 - 2)^{2} } = \sqrt{4 ^{2} } = 4$

Значит AC=BK = 4