Предмет: Геометрия,
автор: kornlosha26
Площа трикутника дорівнює 84 см. Знайти його периметр якщо одна сторона трикутника менша від другої на 1 см а третя більша за другу на 1 см
Ответы
Автор ответа:
4
Ответ:
42 см
Объяснение:
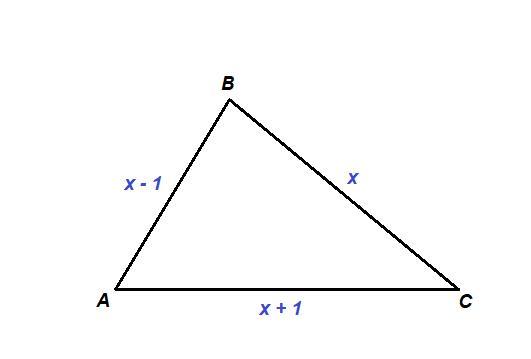
х см - одна сторона треугольника,
(х - 1) см - другая сторона треугольника,
(х + 1) см - третья сторона треугольника.
Тогда полупериметр:
По формуле Герона:
S = 84 см²
не подходит,
(x > 0 по смыслу задачи)
см
ВС = 14 см
АВ = 14 - 1 = 13 см
АС = 14 + 1 = 15 см
Р = 14 + 13 + 15 = 42 см
Приложения:
Похожие вопросы
Предмет: Українська мова,
автор: valyadomanskay
Предмет: Русский язык,
автор: hadabattery
Предмет: Русский язык,
автор: soforen
Предмет: Математика,
автор: zharkunyli
Предмет: История,
автор: Dimka99911