Question

ДОПОМОЖІТЬ БУДЬ ЛАСКА!
Площина α, паралельна основі трапеції, перетинає її бічні сторони AB і CD у точках M і N відповідно. Знайдіть MN, якщо AD = 7 см, BC = 3 см, а AM = BM.

​

Answer 1

Ответ:

MN = 5 см

Объяснение:

Дано: α║BC,AD; α ∩ ABC = MN, M ∈ AB, N ∈ CD, AM = BM, AD = 7 см,

BC = 3 см, ABCD - трапеція

Знайти: MN - ?

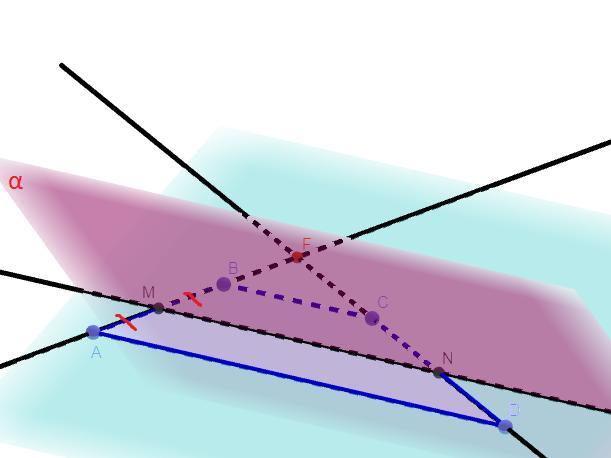
Розв'язання: Подовжимо сторони AB і CD трапеції ABCD. Нехай

AB ∩ CD = F. Так як за умовою α║BC,AD і α ∩ ABC = MN, то MN║BC║AD.За теоремою Фалеса так як MN║BC║AD і AM = BM, то

CN = ND, отже за означенням MN - середня лінія трапеції ABCD. За основною властивістю середньої лінії:

$MN = \dfrac{AD + BC}{2} = \dfrac{7 + 3}{2} = \dfrac{10}{2} = 5$ см.