Question

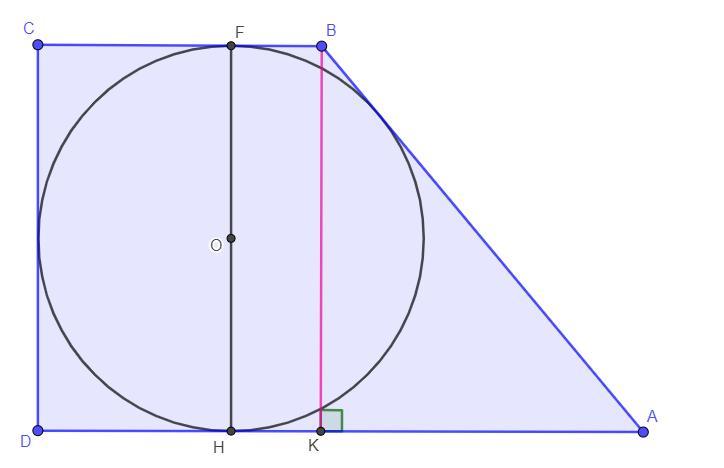
Периметр прямокутної трапеції, описаної навколо кола,
дорівнює 80 см, а її більша бічна сторона дорівнює 30 см.
Знайти радіус кола.

Answer 1

Ответ:

R = 5 см

Объяснение:

Дано: $P_{ABCD} =$ 80 см, AB = 30 см, ABCD - прямокутна трапеція

Знайти: R - ?

Розв'язання: За теоремою якщо чотирикутник можна описати навколо кола, то суми протилежних сторін рівні, отже AB + CD = BC + AD. За означенням периметра трапеції: $P_{ABCD} = AB + BC + CD + AD = AB + CD + AB + CD = 2AB + 2CD$

$P_{ABCD} = 2AB + 2CD|:2$

$AB + CD = \dfrac{P_{ABCD}}{2} = \dfrac{80}{2} = 40$ см.

Проведемо висоту з точки B до основи AD у точку K. Нехай центр O - центр кола вписаного в трапецію. Проведемо висоту яка проходить через точку O, нехай висота перетинає сторону AD в точці H, а сторону BC у точці F. За властивістю прямокутної трапеції її висоти рівні між собою і дорівнють боковій стороні, яка перпендикулярна до основи трапеції, тоді CD = FH = BK. Так як висота FH перетинає трапецію у точках дотика кола за побудовою, то FH - діаметр вписаного кола.

AB + CD = 40 см

AB + BK = 40 ⇒ BK = 40 - AB = 40 - 30 = 10 см

За означенням діаметр кола дорівнює двом радіусам.

Так як FH = BK = 10 см, то R = FH : 2 = 10 : 2 = 5 см.