Question

Определи длину большей боковой стороны прямоугольной трапеции, если один из углов трапеции равен 60°, меньшее основание — 2,7 см, большее основание — 8,8 см.

Ответ: искомая боковая сторона равна ...
см.

Answer 1

Ответ:

СD=12,2 см.

Объяснение:

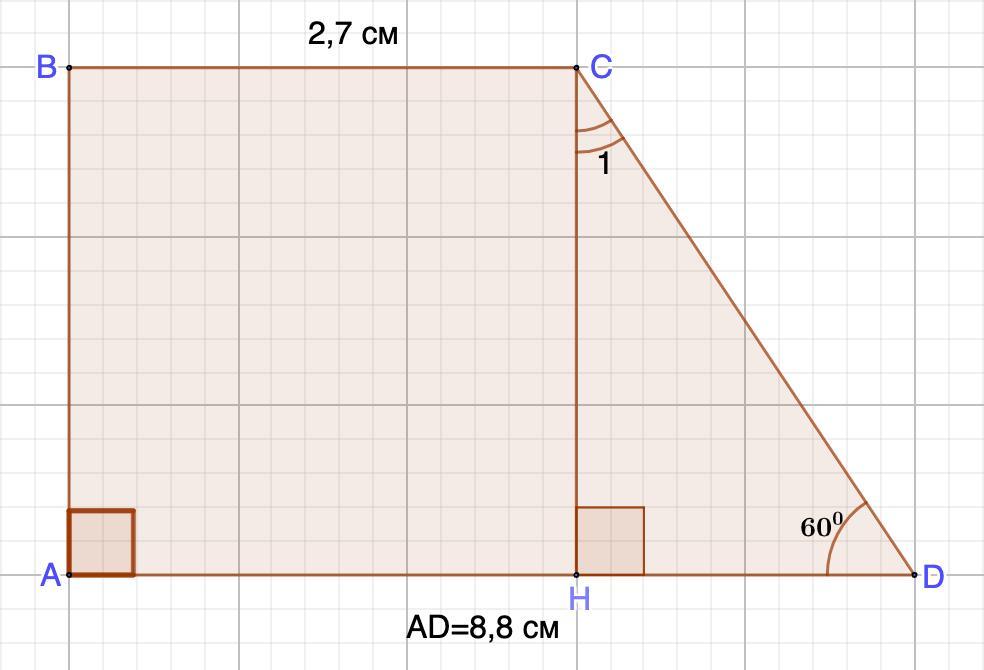
Дано: ABCD - прямоугольная трапеция

∠D=60°

BC=2,7 см; AD=8,8 см.

Найти: CD

Решение:

Проведем СН - высота.

ВС=АН =2,7 см (противоположные стороны прямоугольника равны)

⇒HD=8,8-2,7=6,1 (см)

Рассмотрим ΔНСD - прямоугольный.

Сумма острых углов треугольника равна 90°.

⇒ ∠1=90°-∠D=90°-60°=30°

Катет, лежащий против угла в 30° равен половине гипотенузы.

⇒ СD=НD·2=6,1·2=12,2 (см)