Предмет: Алгебра,
автор: verazh2003
Помогите пожалуйста!! Вычислить sin a, cos a, если tg=-2,4 п/2<a<п
Приложения:
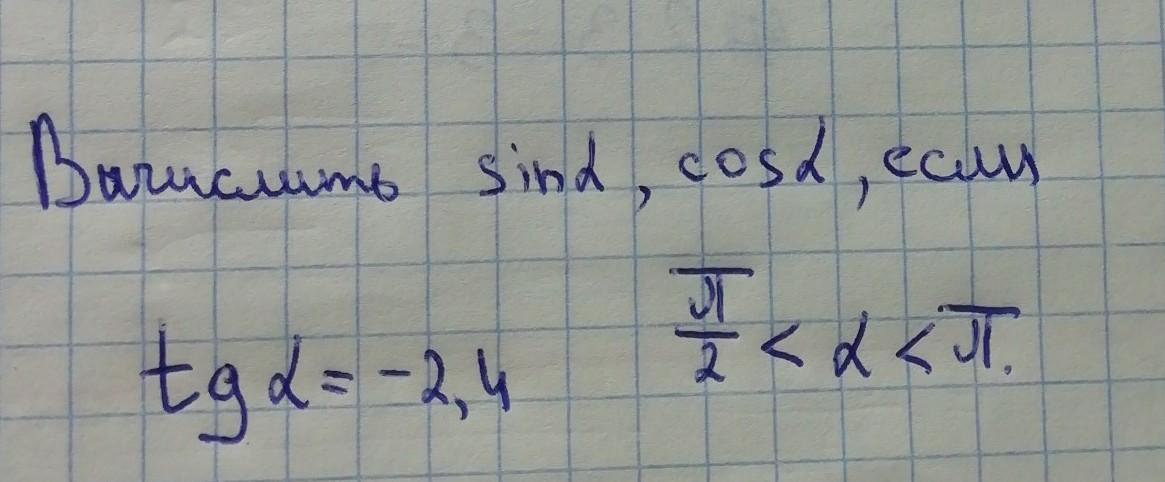
Ответы
Автор ответа:
1
α - угол второй четверти значит Sinα > 0 , a Cosα < 0 .
Похожие вопросы
Предмет: Русский язык,
автор: cofiafgh
Предмет: Английский язык,
автор: Диана12353
Предмет: Русский язык,
автор: zhannaromanova
Предмет: Математика,
автор: Алена24511
Предмет: География,
автор: Anndfg