Предмет: Математика,
автор: Zig284838
Решите уравнение с решением пожалуйста хотябы 3 номера из 5 Прошу Пожалуйста!!!
Приложения:
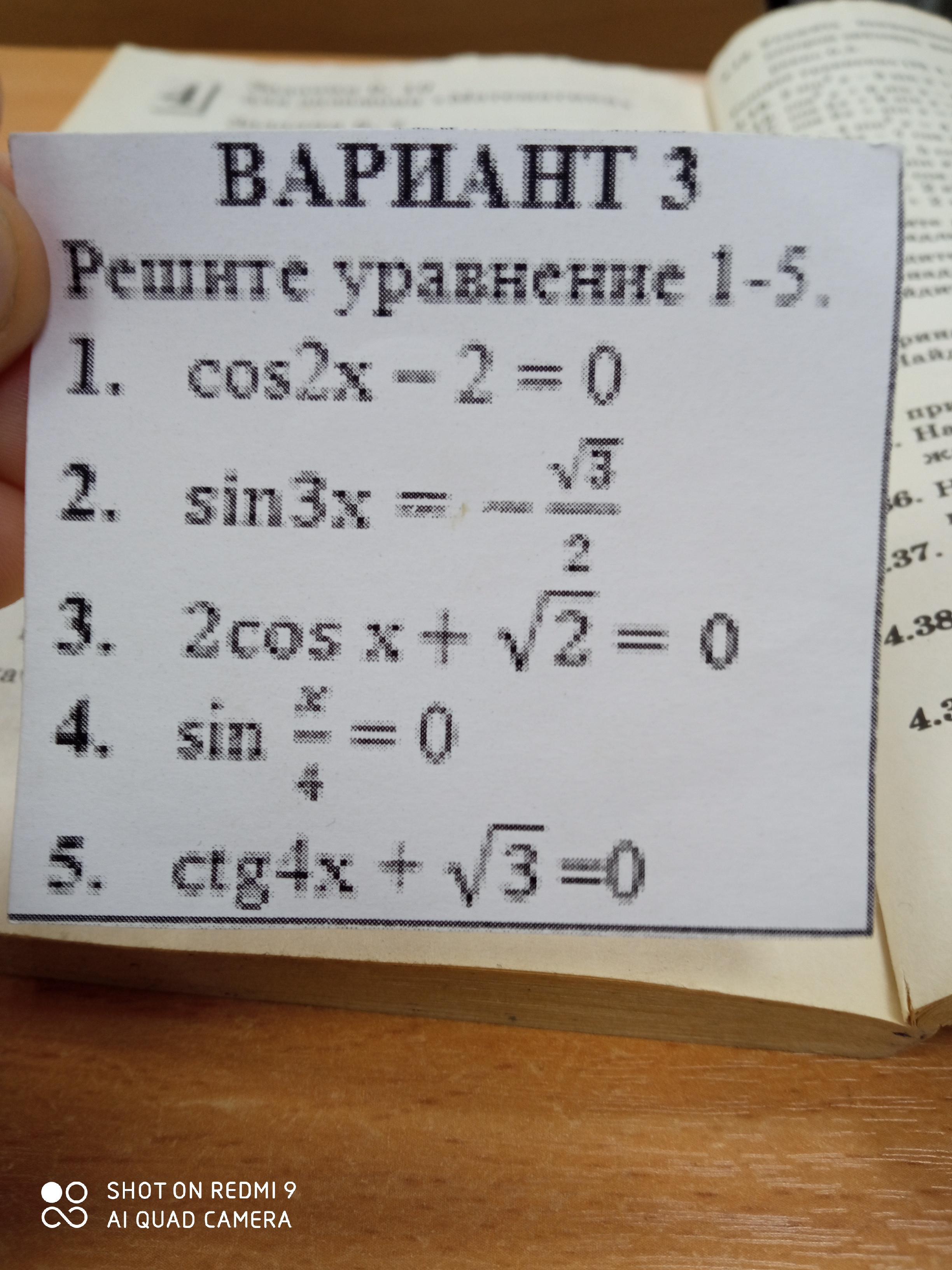
Ответы
Автор ответа:
0
Ответ:
1. cos2x -2 = 0
cos2x = 2
сos = <1 и >-1 =>
=
-
=
2. sin3x = -
3x = 2n +
n = любое целое число.
=
-
=
+
= -
=
3.
2cos x + = 0
2cos (x) = -
2cos (x) = -
x = n -
+ acos (-
)
n = любое целое число.
x = n -
=
=
4. sin = 0
= 2
n - asin (0) +
n = любое целое число.
= 2
ny
= y(2
n +
)
= 0
=
re (y) + i
im (y)
5. -
Пошаговое объяснение:
nikdremov63:
Котангенс((
Похожие вопросы
Предмет: Русский язык,
автор: andrey52rusk
Предмет: Русский язык,
автор: selyunovelena
Предмет: Русский язык,
автор: kposser
Предмет: Математика,
автор: топчик7