Найдите максимальное x⁰+y⁰, где x⁰,y⁰ решение системы уравнений{█(x^2-3xy+3y^2=1@2x^2+xy-y^2=2)┤
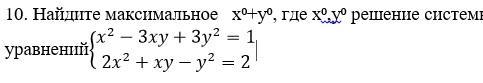
Ответы
Ответ: 2.
Пошаговое объяснение:
Умножим второе уравнение на 3, сложим его с первым уравнением и заменим первое уравнение указанной суммой. После этого получим систему:
7*x²=7
2*x²+xy-y²=2
первое уравнение имеет решения x1=1 и x2=-1, поэтому данная система распадается на две:
x=1
2*x²+xy-y²=2
и
x=-1
2*x²+xy-y²=2
Решим первую систему. Подставляя x=1 во второе уравнение, приходим к уравнению 2+y-y²=2, или y²- y=0. Оно имеет решения y=0 и y=1, поэтому первая пара решений исходной системы такова:
x=1, y=0 и x=1, y=1
Решим вторую систему. Подставляя x=-1 во второе уравнение, приходим к уравнению 2-y-y²=2, или y²+ y=0. Оно имеет решения y=0 и y=-1, поэтому вторая пара решений исходной системы такова:
x=-1, y=0 и x=-1, y=-1
Таким образом, исходная система имеет 4 пары решений:
x=1, y=0; x=1, y=1; x=-1, y=0; x=-1, y=-1.
Отсюда наибольшее значение суммы решений равно 1+1=2.