Question

50 балов!!!
решите побыстрее

Answer 1

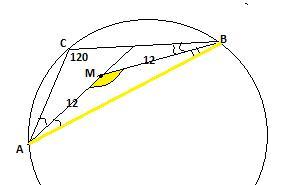
В ΔАВС известно , что ∠С=120° , М-точка пересечения биссектрис. Радиус описанной около ΔАВС , равен 12 см.Найдите радиус  окружности , описанной около ΔАМВ.

Объяснение:

Анализ.

1) Для нахождения радиуса описанной окружности можно использовать т. синусов;

2) Тогда для ΔАМВ необходимо знать хотя бы одну сторону и противолежащий угол.

Решение.

а) ΔАВС . Т.к. М-точка пересечения биссектрис , то М-центр описанной окружности  ⇒ МА=МС=МВ=R(ΔАВС)=12 см.

По т. синусов   $\frac{AB}{sin C} =2R$  ,  $\frac{AB}{sin 120} =2*12$  ,   $\frac{AB}{ \frac{\sqrt{3} }{2} } =24 ,$  ,     AB=12√3 см.

б)ΔАВС , по т. о сумме углов треугольника ∠А+∠В=180°-120°=60°. Но АМ, ВМ-биссектрисы, поэтому ∠МАВ+∠МВА=60°:2=30°.

в)ΔАМВ , ∠АМВ=180°-30°=150° . По т. синусов     $\frac{AB}{sin AMB} =$2R(ΔAMB)  ,

$\frac{12\sqrt{3} }{sin 150} =$ 2R ,    $\frac{12\sqrt{3} }{0,5} =$ 2R  , R=12√3 см.