Предмет: Алгебра,
автор: Аноним
помогите пожалуйста
Приложения:
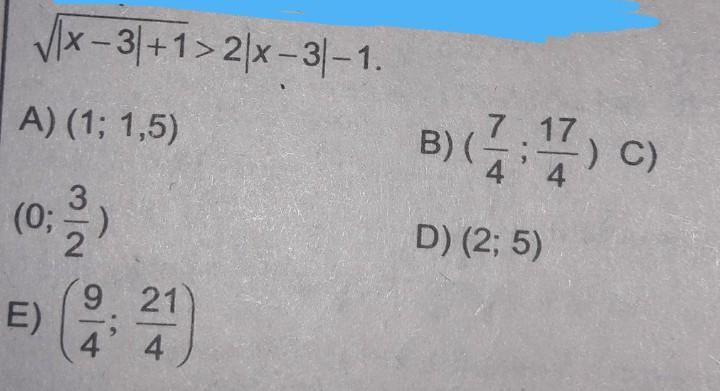
Ответы
Автор ответа:
1
Обозначим неравенство принимает вид
Учитывая, что существенным является только неравенство
Ответ: B
Замечание. Мы не учитывали неотрицательность подкоренного выражения, поскольку его неотрицательность для всех значений аргумента изначально очевидна.
Похожие вопросы
Предмет: Українська мова,
автор: tomoxazp
Предмет: Русский язык,
автор: svarkaasb
Предмет: Русский язык,
автор: justaforever
Предмет: Физика,
автор: 1038879292273738
Предмет: Физика,
автор: Response