Предмет: Алгебра,
автор: asssass222
Решите интергал, даю 15 баллов
Приложения:
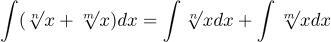
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Русский язык,
автор: sonia27112006
Предмет: Українська мова,
автор: mazepaivan2016
Предмет: Русский язык,
автор: grushevskaya
Предмет: Литература,
автор: karinakhakimova14
Предмет: Обществознание,
автор: voevkate4