Предмет: Алгебра,
автор: slaviksheregi17
розвязати рівняння
тема:дробові рівняння
Приложения:
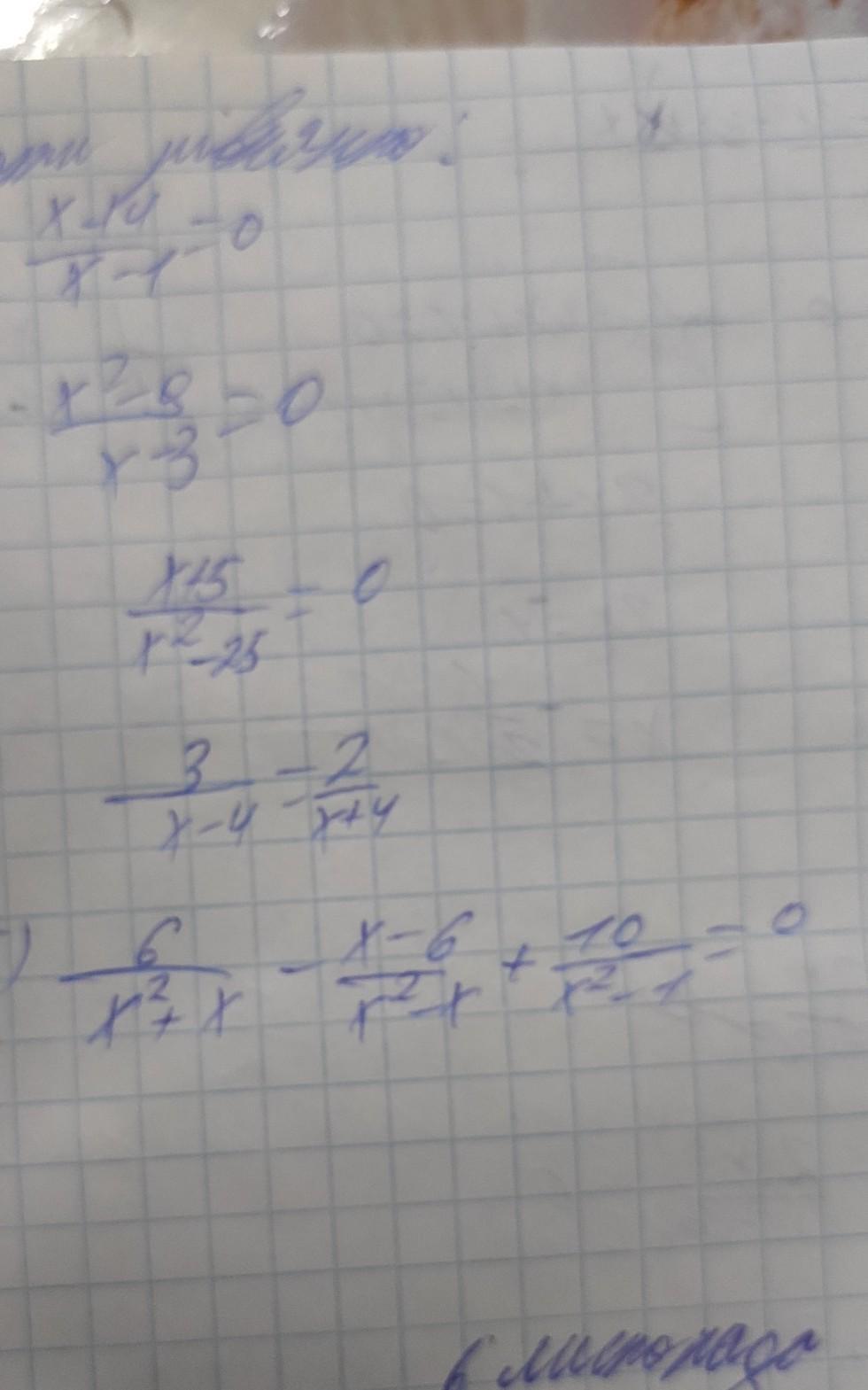
Ответы
Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: Другие предметы,
автор: vipikirya
Предмет: Русский язык,
автор: trem74
Предмет: Русский язык,
автор: lindsi1
Предмет: Математика,
автор: Мария111111111мнпв
Предмет: Математика,
автор: ariana2307