Здравствуйте, помогите пожалуйста
Ответы
Ответ:
Объяснение:
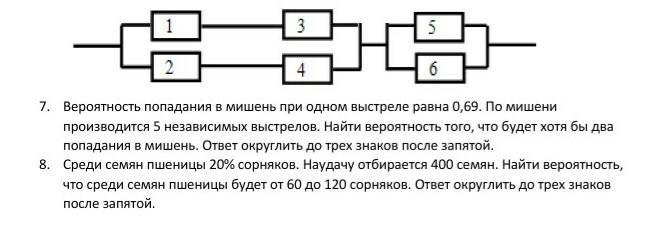
7. Вероятность попадания в мишень при одном выстреле p = 0,69.
Значит, вероятность промаха q = 1 - p = 1 - 0,69 = 0,31.
Количество выстрелов n = 5. Количество попаданий: хотя бы m = 2.
Значит, надо рассмотреть случаи 2, 3, 4 и 5 попаданий.
1) 2 попадания, 3 промаха. По формуле Бернулли:
P(2) = C(2,5)*p^2*q^3 = 5*4/2*0,69^2*0,31^3 ≈ 0,1418
2) 3 попадания, 2 промаха. По формуле Бернулли:
P(3) = C(3,5)*p^3*q^2 = 5*4*3/(2*3)*0,69^3*0,31^2 ≈ 0,3157
3) 4 попадания, 1 промах. По формуле Бернулли:
P(4) = C(4,5)*p^4*q^1 = 5*0,69^4*0,31^1 ≈ 0,3513
4) 5 попаданий, 0 промахов. По формуле Бернулли:
P(5) = C(5,5)*p^5*q^0 = 1*0,69^5*1 ≈ 0,1564
Нужная нам вероятность равна сумме этих вероятностей:
P = P(2) + P(3) + P(4) + P(5) = 0,1418+0,3157+0,3513+0,1564 = 0,9652 ≈ 0,965
8. Это по интегральной теореме Муавра - Лапласа.
Среди семян 20% сорняков. Вероятность найти сорняк p = 0,2.
Вероятность найти пшеницу q = 1 - p = 1 - 0,2 = 0,8.
Всего семян n = 400. Сорняков должно быть от m1 = 60 до m2 = 120.
P(m1<x<m2) = Ф(x2) - Ф(x1)
Значения интегральной функции Лапласа Ф(x) берем из таблиц.
P(m1<x<m2) = Ф(x2) - Ф(x1) = 0,499997 - (-0,4938) = 0,993797 ≈ 0,994
P = P(2) + P(3) + P(4) + P(5)
а по формуле
P = 1 - P(0) - P(1)