помогите пожалуйста с математикой

Ответы
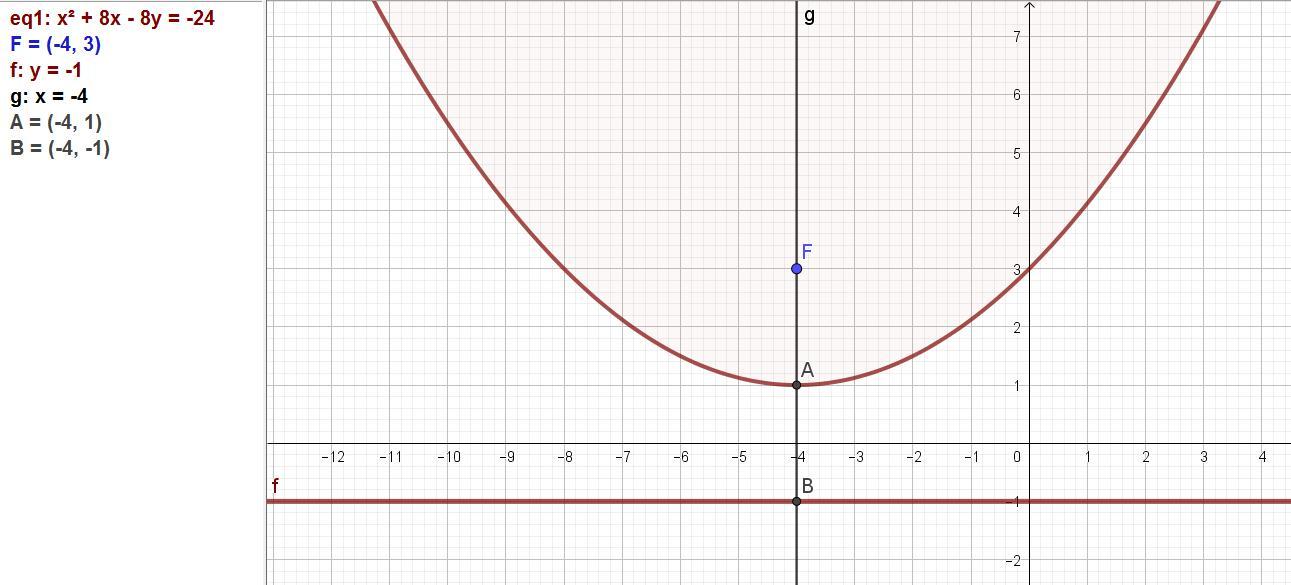
2) Дано: точка A(-4; 3) и прямая y = -1. Необходимо составить уравнение геометрического места точек, равноудаленных от заданной точки и прямой.
Пусть точка, соответствующая заданным требованиям, М(х; у).
Расстояние АМ² = (х - (-4))² + (у - 3)² = (х + 4)² + (у - 3)².
Так как по заданию расстояние АМ равно (у - (-1)), то подставим это значение в уравнение.
(y + 1)² = (x + 4)² + (у - 3)². Раскроем скобки с переменной у.
у² + 2y + 1 = (x + 4)² + у² - 6y + 9. Приводим подобные.
(x + 4)² = 8y - 8.
(x + 4)² = 2*4*(y - 1).
Получено уравнение параболы, ось которой параллельна оси Оу.
Вершина в точке (-4; 1). Параметр р = 4.
Можно преобразовать это уравнение относительно у.
(x + 4)² = 8y - 8,
x² + 8х + 16 = 8y - 8,
8у = x² + 8х +24,
у = (1/8)x² + х + 3.
3) Решение СЛАУ методом Крамера.
x1 x2 x3 B 4
2 -3 2 10 Определитель
1 -2 1 7
3 2 -1 1
Заменяем 1-й столбец на вектор результатов B:
10 -3 2 8
7 -2 1 Определитель
1 2 -1
Заменяем 2-й столбец на вектор результатов B:
2 10 2 -16
1 7 1 Определитель
3 1 -1
Заменяем 3-й столбец на вектор результатов B:
2 -3 10 -12
1 -2 7 Определитель
3 2 1
x1= 8 / 4 = 2
x2= -16 / 4 = -4
x3= -12/ 4 = -3.
Находить определитель проще всего по треугольной схеме.
Вот первый.
2 -3 2| 2 -3
1 -2 1| 1 -2
3 2 -1| 3 2 =
= 4 -9 4
-3 -4 12 = 4.