Question

Дам 12 баллов. Прошу, помогите если вам не трудно.
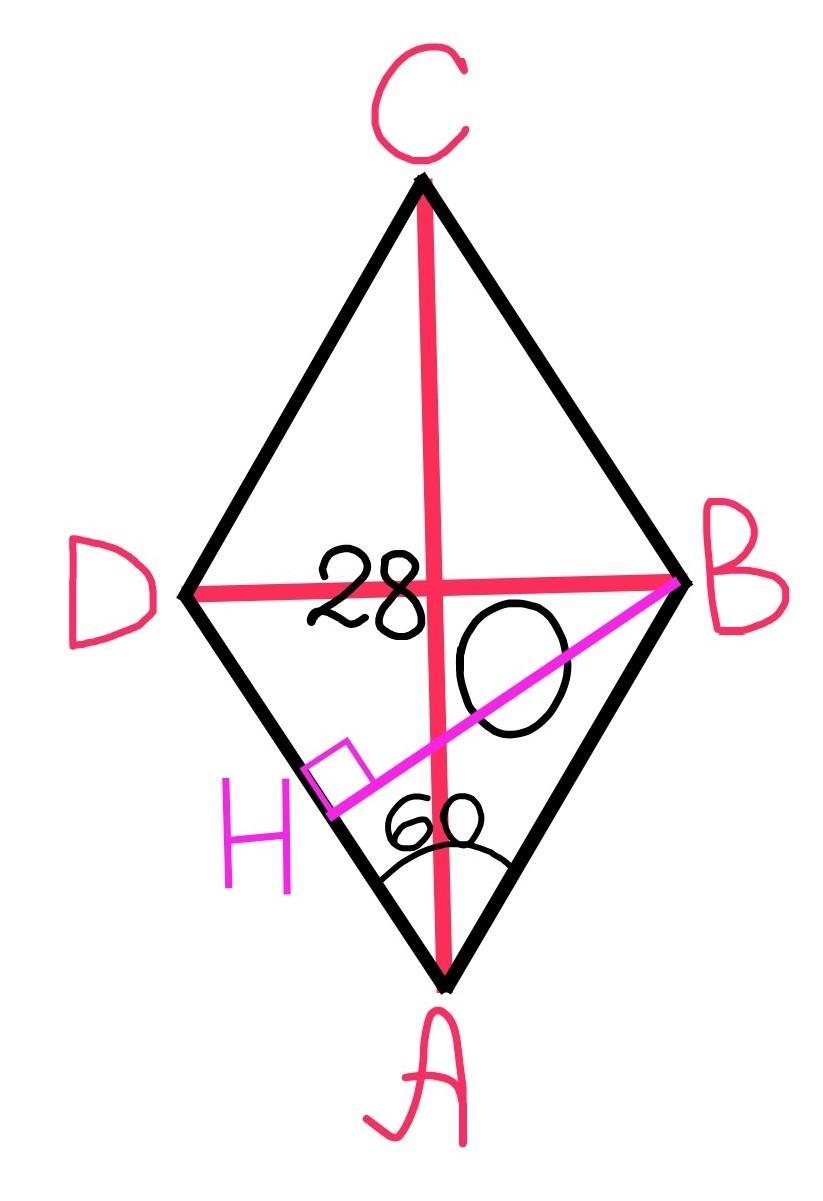
В ромбе ABCD ∠A=60ᴼ, AC=28 и диагонали пересекаются в т. О. Найдите
высоту ромба.

Answer 1

Ответ:

Рассмотрим ∆ВОА и ∆ВНА.

АВ – общая сторона;

Диагонали ромба пересекаясь образуют 4 прямых угла и точкой пересечения делятся пополам.

Следовательно угол АОВ=90°, тоесть ∆ВОА – прямоугольный с прямым углом ВОА, и АО=АС÷2=28÷2=14.

Угол ВНА=90°, так как ВН – высота;

Угол BAD=60° по условию;

Углы при одной стороне ромба в сумме равны 180°.

Тогда угол АВС=180°–угол BAD=180°–60°=120°

Диагонали ромба являются биссектрисами его углов. Исходя из этого: угол DBA=угол АВС÷2=120°÷2=60°

Получим что ∆ВОА=∆ВНА как прямоугольные треугольники с равными острым углом и катетом.

Тогда АО=ВН как соответственные стороны, следовательно ВН=14.

Ответ: 14