Предмет: Алгебра,
автор: AnnaCrau
Помогите пожалуйста!!!!!
Приложения:
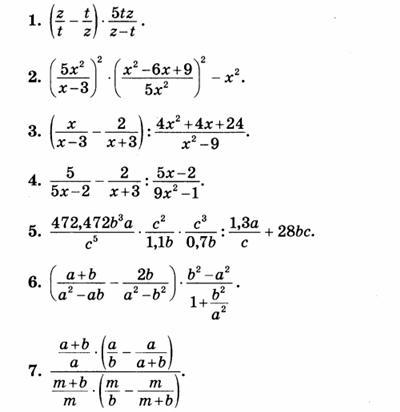
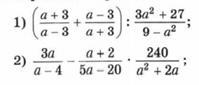
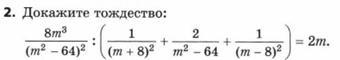
Rakvium:
Ого. Лучше бы такое отдельными вопросами кидать, - быстрее будет, но я возьмусь :)
Ответы
Автор ответа:
1
Решение заданий с первого изображения:
Решение заданий со второго изображения:
Доказательство тождества с третьего изображения:
Похожие вопросы
Предмет: Русский язык,
автор: виканикалика
Предмет: Русский язык,
автор: omghappily
Предмет: Английский язык,
автор: ekaterinas20001
Предмет: Литература,
автор: Литлэст
Предмет: Алгебра,
автор: бабочка132