Предмет: Математика,
автор: tigaiilya
помогите решить
Срочно дам 20 баллов
Приложения:
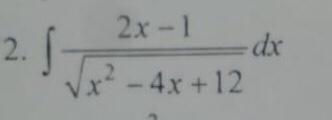
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Приложения:

Автор ответа:
0
Ответ:
Пошаговое объяснение:
Интеграл разобьем на два
Замечая, что , перепишем первый интеграл
Перепишем подинтегральную функцию для второго интеграла, как
Тогда интеграл запишется, как
это гиперболический арксинус
Ответ :
Проверяем себя в Maxima
Приложения:
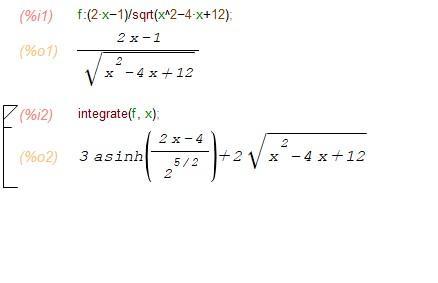
Похожие вопросы
Предмет: Русский язык,
автор: valeryivanova
Предмет: Другие предметы,
автор: kamilkarimmal
Предмет: Қазақ тiлi,
автор: dklobuk
Предмет: Математика,
автор: Semen144