Question

В трапеции ABCD боковые стороны AB и CD равны,CH-высота,проведённая к большему основанию AD.Найдите длину отрезка HD,если средняя линия KM трапеции равна 10,а меньшая основанию BC равна 4

Answer 1

Ответ:

6 ед. изм.

Объяснение:

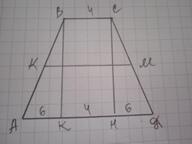
ДАНО: ABCD - трапеция,  AB=CD, СН - высота, КМ - средняя линия, КМ=10, ВС=4. Найти НD.

Средняя линия трапеции равна полусумме оснований.

КМ=(ВС+АD)/2;  10=(4+АD)/2;  4+АD=20;  АD=16.

Проведем вторую высоту ВК.

КН=ВС=4;  

ΔАВК=ΔСDН по катету и гипотенузе, значит АК=DН=(16-4)/2=6.