Предмет: Геометрия,
автор: Нейтральняшка
M — середина стороны BC равностороннего треугольника ABC. Точки D и E на сторонах AB и AC соответственно таковы, что ∠DME=60∘. Найдите BD+CE, если AB=17, DE=10
Simba2017:
это что?
не из учебника...
систему уравнений для сторон малого треугольника пишите
хотя может и геометрически как можно....
нет, все проще, там треугольники равные будут и ответ 17
неверно тогда наверное...
я нашла свою ошибку...
Ответы
Автор ответа:
12
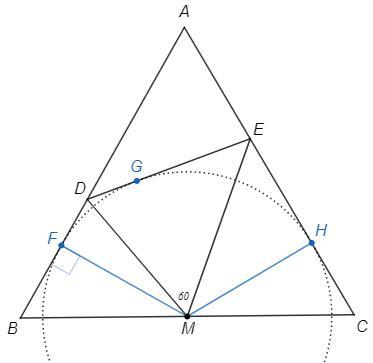
Точка M лежит на биссектрисе угла A (в равностороннем треугольнике медиана является биссектрисой).
Кроме того, отрезок DE виден из точки M под углом 90 -A/2.
Следовательно M - центр вневписанной окружности треугольника DAE.
F, G, H - точки касания
DF=DG, EH=EG (отрезки касательных из одной точки)
BF=CH =BM/2 (катет против угла 30)
BD+CE =BF+CH+DF+EH =2BM/2 +(DG+EG) =BM+DE =8,5+10 =18,5
Приложения:
я решала проще, но у меня ответ другой
да, у вас все верно, спасибо!
похожая задача: https://znanija.com/task/33947782
да, только не все школьники знают о вневписанных окружностях...
там все же можно через подобие решить, но долго...
Спасибо!
Похожие вопросы
Предмет: Русский язык,
автор: Doszhan93
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: senyanet
Предмет: Математика,
автор: Аноним
Предмет: Геометрия,
автор: F1x3r