Предмет: Алгебра,
автор: aruzhantuleuova
найти значение производной функции f (x) в точке, где абсцисса x0
Приложения:
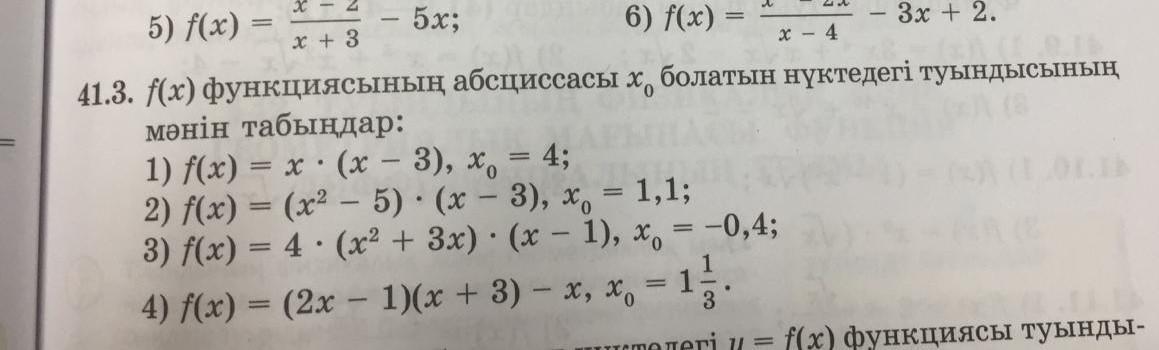
Simba2017:
проверьте еще все мои вычисления
Ответы
Автор ответа:
2
1)f`(x)=x-3+x=2x-3
f`(4)=8-3=5
2)f`(x)=2x(x-3)+(x^2-5)*1=2x^2-6x+x^2-5=3x^2-6x-5
f`(1.1)=3*1.21-6.6-5=-7.97
3)f`(x)=4((2x+3)(x-1)+x^2+3x)=4(2x^2+x-3+x^2+3x)=4(3x^2+4x-3)=12x^2+16x-12
f`(-0.4)=12*0.16-16*0.4-12=1.92-6.4-12=-16.48
4)f`(x)=2(x+3)+2x-1-1=4x+4
f`(4/3)=4*4/3+4=5 1/3+4=9 1/3
ок, спасибо огромное!♡♡♡
у меня вычислительные ошибки при подстановке, отметьте нарушение
Автор ответа:
1
спасибо большое!!!
во втором у вас тоже ....
перед квадратом 3 на 2 сменилась
исправила ...
Похожие вопросы
Предмет: Русский язык,
автор: knopka63reg
Предмет: Русский язык,
автор: АрхАнгеЛика
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: Рубин121
Предмет: История,
автор: shar1983