Предмет: Алгебра,
автор: restIess
Вычислить предел функции не используя метод Лопиталя
Приложения:
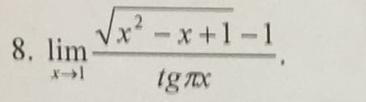
Ответы
Автор ответа:
3
Ответ:
Объяснение:
!!!!!!!!!!!!!!!!!!!!!!!
Приложения:

Аноним:
У вас ошибка. Косинус пи равен не 1 а -1, тогда ответ отрицательный!
https://prnt.sc/ve5jvu
Стоп, т стремится к 0
Отмена, где-то в другом ошибка
Полная отмена, извиняюсь, ошибки не было
Автор ответа:
6
Ответ:
Объяснение:
1 Запишем
2 Умножим на 1
Представим 1 как дробь
3 Соберем все в одну дробь
4 В числителе разность квадратов
где
5 Упростим числитель и представим предел произведения как произведение пределов
6 Можно посчитать первый предел
7 Представим тангенс как отношение синуса и косинуса
8 Вынесем косинус и посчитаем
9 Разложим на множители числитель
10 Умножим на 1
Представим 1 как отношение
11 Вынесем пи
12 Перед нами первый замечательный предел, так как
при
при
ОТВЕТ
Похожие вопросы
Предмет: Английский язык,
автор: ngrdana
Предмет: Другие предметы,
автор: Аноним
Предмет: Английский язык,
автор: ENZHE62
Предмет: Математика,
автор: Aymanak13
Предмет: Литература,
автор: nikb95