Предмет: Алгебра,
автор: TheStrike666
Решите неравенство. Можете написать только область допустимых значений? И ответ будет промежутком? Или просто писать, чему равен х?
Приложения:
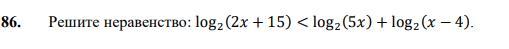
Ответы
Автор ответа:
1
tamarabernukho:
..
Автор ответа:
1
Объяснение:
ОДЗ:
-∞__+__-0,6__-__5__+__+∞ ⇒
x∈(-∞;-0,6)U(5;+∞).
Согласно ОДЗ:
Ответ: х∈(5;+∞).
Похожие вопросы
Предмет: Другие предметы,
автор: Arhipka0677
Предмет: Русский язык,
автор: sashoko
Предмет: Другие предметы,
автор: olgakapralova1
Предмет: Биология,
автор: Liza121011