Предмет: Математика,
автор: ekaterina2352
помогите с математикой. вариант 1Б. Хотя бы частично. Заранее спасибо
Приложения:
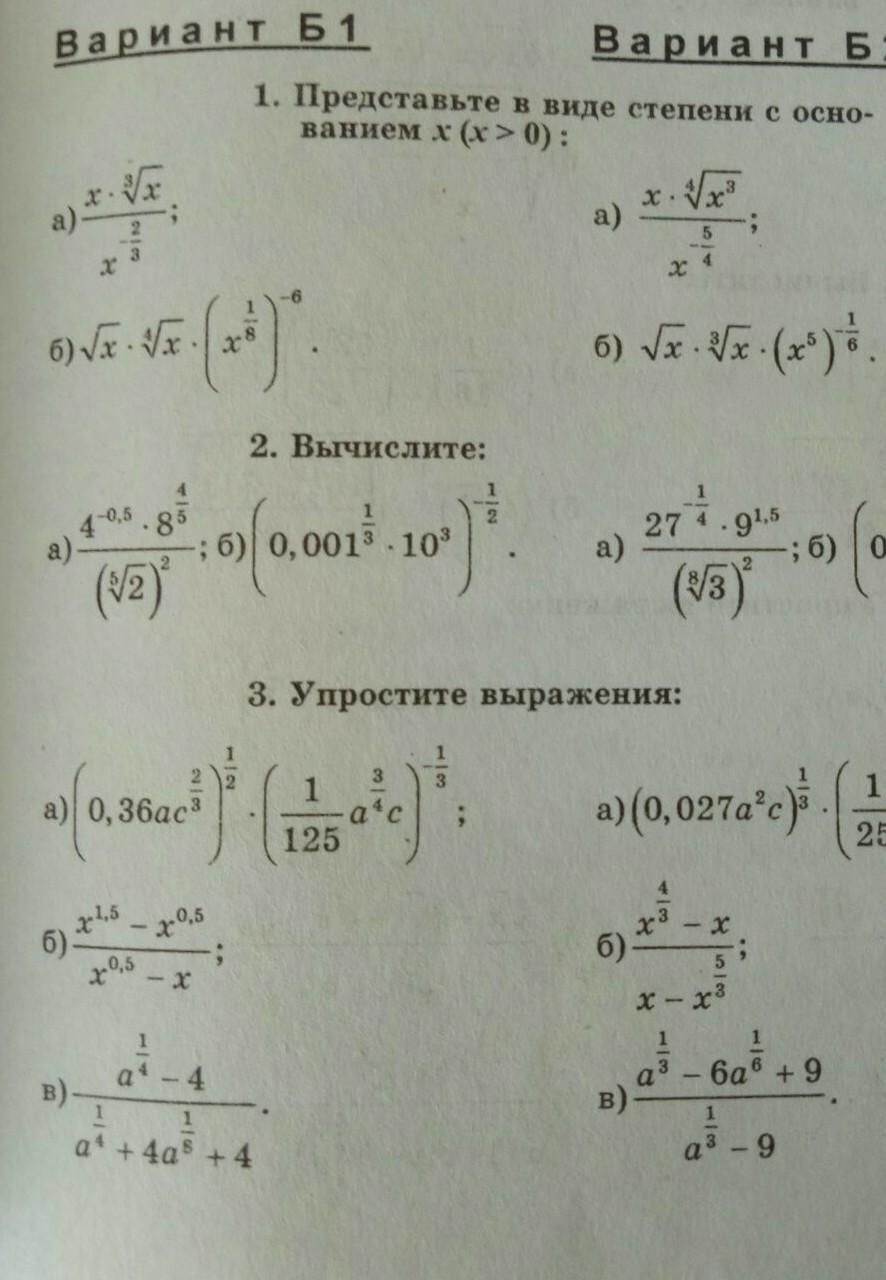
Ответы
Автор ответа:
1
Задание 1
а)
б)
Задание 2
а)
б)
Задание 3 a)
б)
в)
ekaterina2352:
спасибо огромное
Похожие вопросы
Предмет: Русский язык,
автор: Алекся12
Предмет: Русский язык,
автор: kadochnikov200
Предмет: Русский язык,
автор: Nikitka101
Предмет: История,
автор: ксюха2701