Предмет: Математика,
автор: Fufix
Найти частное решение дифференциального уравнения, удовлетворяющее
заданным начальным условиям:
Приложения:
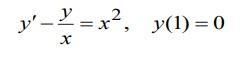
Ответы
Автор ответа:
2
Возьмите производную
Дефферицировать
Использовать правила дефферицирования
Упростить
Деференцировать
Вычеслите произведение
Умножить обе части
Раскрыть скобки
Перенесите слагаемые в др часть уравнения
Разложите выражение на множители
Разделите обе стороны
2) у=0
Похожие вопросы
Предмет: Русский язык,
автор: elen1982
Предмет: Английский язык,
автор: asadchihmv
Предмет: Русский язык,
автор: solozhentseva79
Предмет: Математика,
автор: ЮлияЧерник