Предмет: Алгебра,
автор: kreez3221
Вычислить предел функции.
Приложения:
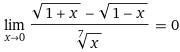
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Русский язык,
автор: hfgiyy
Предмет: Русский язык,
автор: loveverone
Предмет: Русский язык,
автор: lubimtseva0409
Предмет: Музыка,
автор: kuleshovaa2017
Предмет: Обществознание,
автор: ildarmyha58Wolf