Предмет: Математика,
автор: Infalible
30 БАЛОВ!!
С помощью интегральной формулы Коши или формулы типа Коши вычислить:
Приложения:
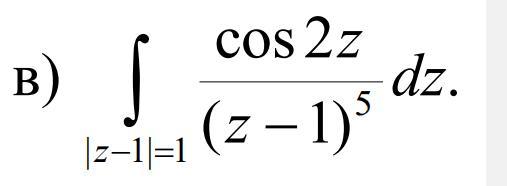
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Подынтегральная функция имеет один ноль , при этом он лежит в области
(
) и имеет кратность 5.
, при этом
, очевидно, аналитическая в области
, ограниченной указанным контуром (т.к. аналитическая на всей комплексной плоскости), а
- полином, не имеющий нулей на контуре
.
Тогда
Infalible:
Спасибо огромное Вам!
Похожие вопросы
Предмет: Русский язык,
автор: Egorxxx
Предмет: Английский язык,
автор: eremenko2001
Предмет: Русский язык,
автор: denshlomov
Предмет: ОБЖ,
автор: KIRILL64142