Предмет: Геометрия,
автор: kladovaulia01
Прямоугольный треугольник, гипотенуза которого равна с, повернут около вершины прямого угла на 90°. Найдите сумму площадей, описанных при этом катетами.
Помогите пжжж
siestarjoki:
один катет повернулся на четвертинку и другой на четвертинку
п a^2/4 + п b^2/4 =п/4 (a^2+b^2) =п c^2/4
спасибо
Ответы
Автор ответа:
1
При повороте на 90 относительно С точка A переходит в A'.
Поворот является движением, расстояния между точками не изменяются.
Следовательно точка A описала дугу 90 окружности радиуса AC.
След катета AC - 1/4 окружности радиуса AC.
Аналогично след катета BC - 1/4 окружности радиуса BC.
1/4 п AC^2 + 1/4 п BC^2/4 =1/4 п (a^2 +b^2) =п c^2 /4
Приложения:
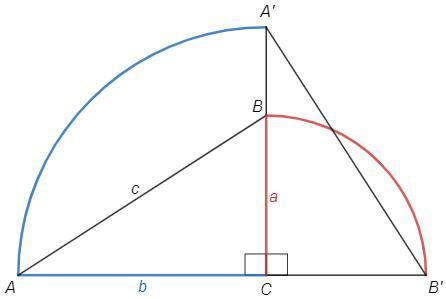
заметим, что с/2 - радиус описанной окружности ABC
спасибо большое, другу очень надо
можно сказать, что искомая площадь равна площади описанной окружности ABC.
Похожие вопросы
Предмет: Русский язык,
автор: olyadavidenko
Предмет: Русский язык,
автор: nawpa25
Предмет: Английский язык,
автор: Skazkamgn
Предмет: Математика,
автор: JeffPozitiv