Предмет: Математика,
автор: Valer26
Plizzzz помогите пожалуйста
Приложения:
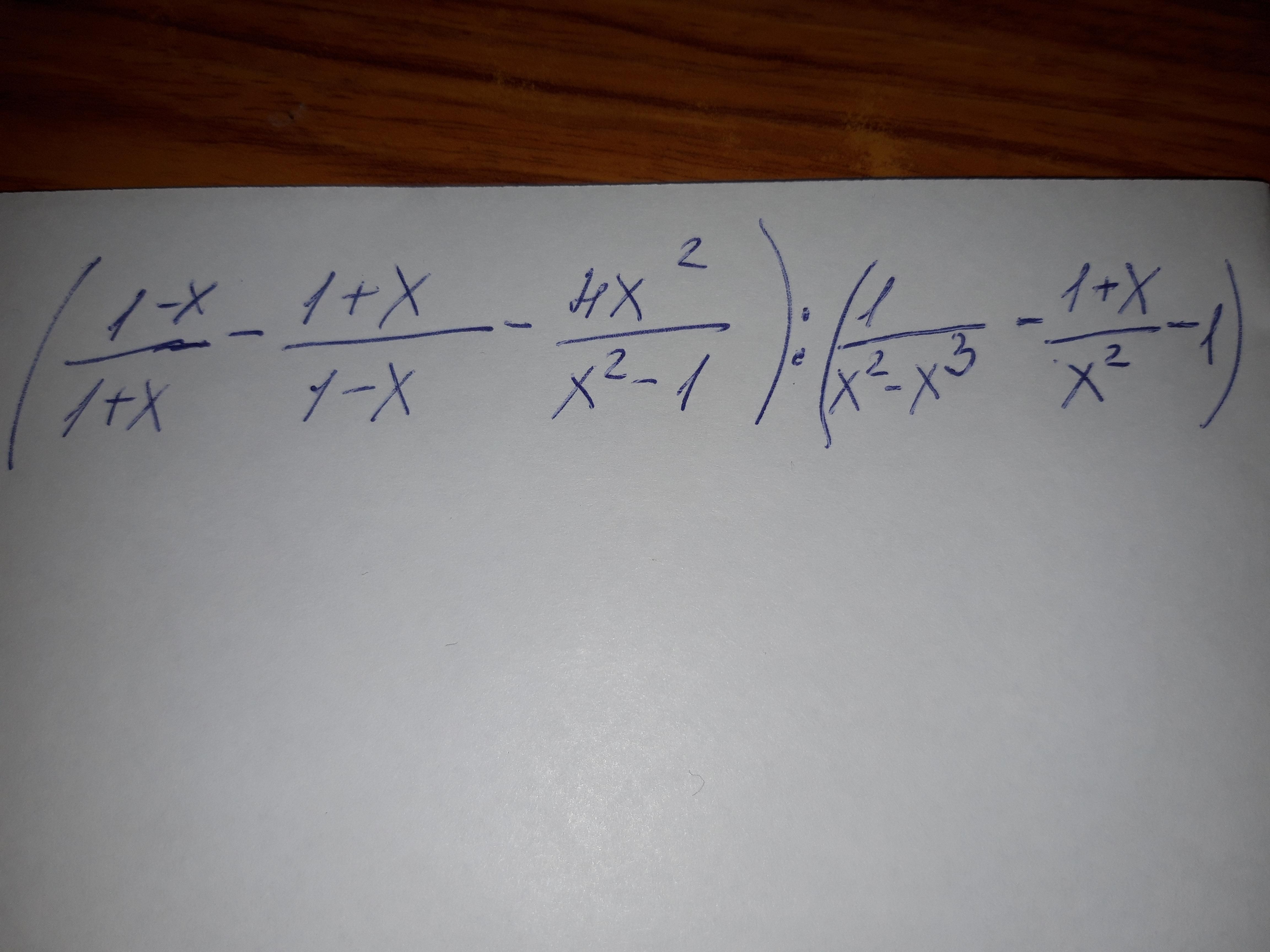
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Не уверена, но что успела...
Приложения:

Автор ответа:
1
Ответ:
Пошаговое объяснение:
Похожие вопросы
Предмет: Другие предметы,
автор: galinka111391
Предмет: Русский язык,
автор: natashabayurova
Предмет: Английский язык,
автор: katea13
Предмет: История,
автор: alisa72006
Предмет: Физика,
автор: SanekBoton