Question

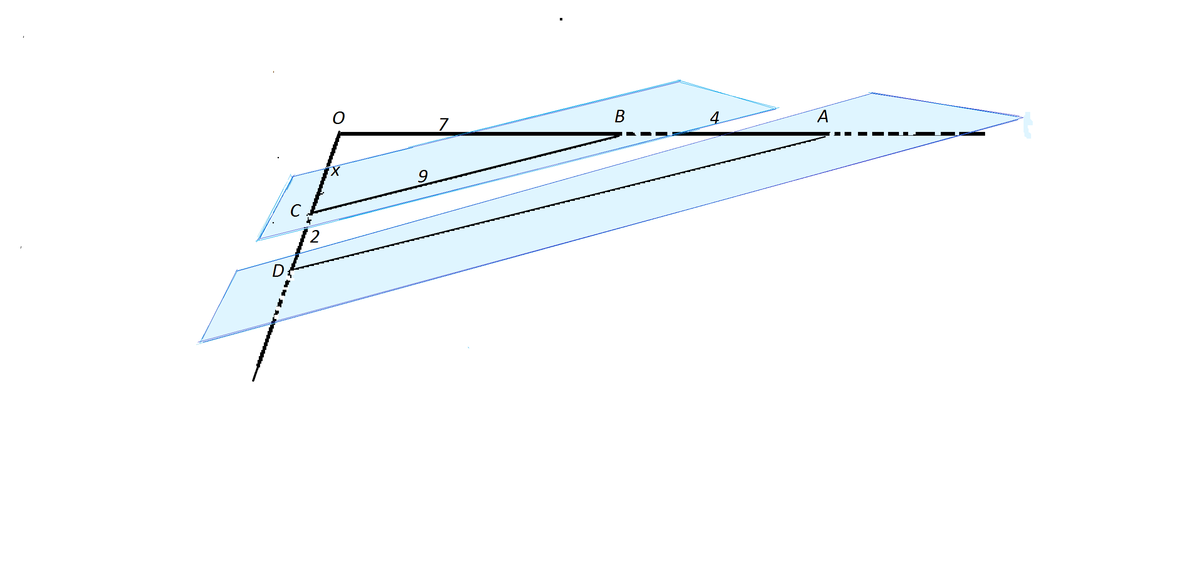
Дан угол AOD и две параллельные плоскости α и β. Плоскость α пересекает стороны угла OA и OD соответственно в точках A и D, плоскость β эти стороны пересекает соответственно в точках B и C. Дано: OB = 7 AB = 4 BC = 9 CD = 2

Найти: AD OD

Answer 1

Нарисуем угол и линии СВ и АД пересечения с плоскостями. 
Мы получили два подобных треугольника ДОА и СОВ, т.к. угол О в них общий, а стороны СВ и АД параллельны, и по этой причине соответственные углы при этих сторонах равны.  
Найдем коэффициент подобия этих треугольников. 
АО:ВО=(7+4):7=11/7 
Отсюда следует отношение ДО:СО=11/7 
ДО=2+х 
(2+х):х=11/7 
Решив это уравнение/, получим длину СО=3,5 
ОД=СД+Ос=2+3,5=5,5
 АД:ВС=11/7 
АД:9=11/77
АД=99/7= 14 и 1/7