Question

вершины треугольника делят описанную около него окружность на три дуги длины которых относятся как 6: 11: 19 найдите радиус окружности если меньшая из сторон равна 15​

Answer 1

Ответ:

15

Пошаговое объяснение:

Пусть х - коэффициент пропорциональности. Тогда

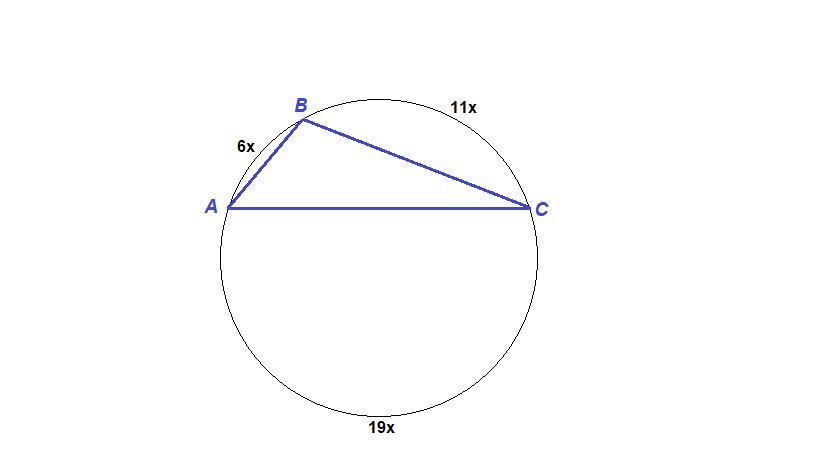
∪АВ = 6х,  ∪ВС = 11х,  ∪АС = 19х.

Полная окружность составляет 360°:

6x + 11x + 19x = 360°

36x = 360°

x = 10°

∪АВ = 60°,  ∪ВС = 110°,  ∪АС = 190°.

Углы треугольника вписанные, поэтому они равны половине соответствующих дуг:

∠АСВ = 1/2 ∪АВ = 30°

∠ВАС = 1/2 ∪ВС = 55°

∠АВС = 1/2 ∪АС = 95°

В треугольнике против меньшего угла лежит меньшая сторона,

АВ = 15.

По следствию из теоремы синусов:

$\dfrac{AB}{\sin C}=2R$

$R=\dfrac{AB}{2\sin C}=\dfrac{15}{2\cdot \sin 30^\circ}=\dfrac{15}{2\cdot \frac{1}{2}}=15$