Предмет: Математика,
автор: m4n0sov
Помогите пожалуйста. Задание: продифферинцировать функции
Приложения:
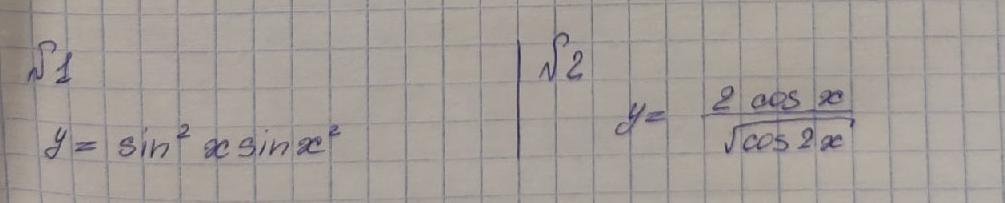
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Русский язык,
автор: jakovlevVladik
Предмет: Русский язык,
автор: lololplpa
Предмет: Русский язык,
автор: anyaulyanitskaya
Предмет: Математика,
автор: 12345678909876567
Предмет: Алгебра,
автор: xxx20001