Предмет: Алгебра,
автор: tv911648
Помогите, пожалуйста, решить БЕЗ Лопиталя
Приложения:
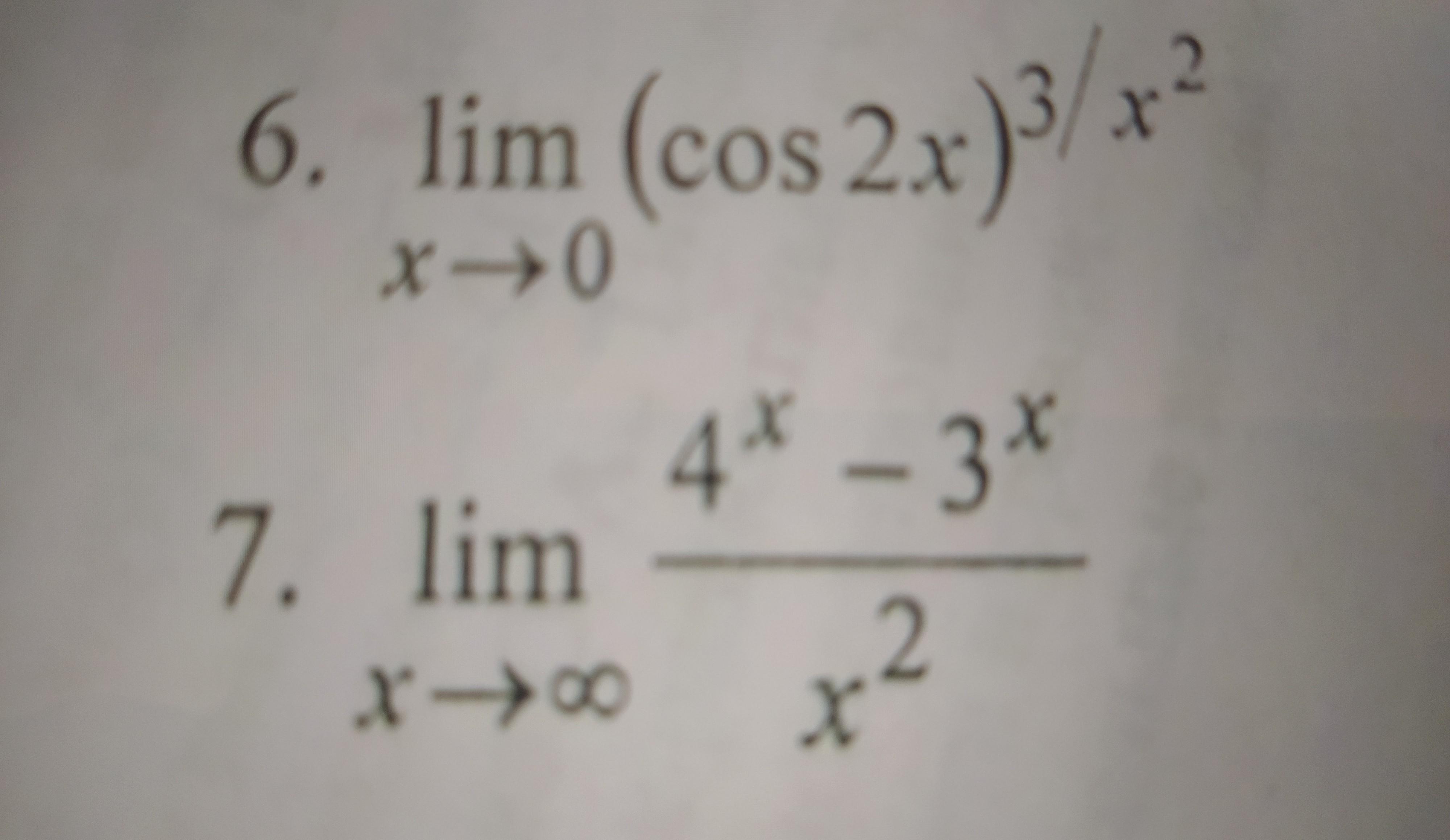
Ответы
Автор ответа:
1
Бесконечно большая показательная функция при
стремиться к
быстрее, чем степенная функция
, поэтому при
предел равен
. При
можно написать так:
. Поэтому ответ такой:
tv911648:
Спасибо! Очень помогли
Похожие вопросы
Предмет: Русский язык,
автор: Zippo133729
Предмет: Русский язык,
автор: bulatov22
Предмет: Русский язык,
автор: kurbana
Предмет: Литература,
автор: lenapolyanskay
Предмет: Математика,
автор: eltinua