Предмет: Алгебра,
автор: gdfsf
найти область определения функции
Приложения:
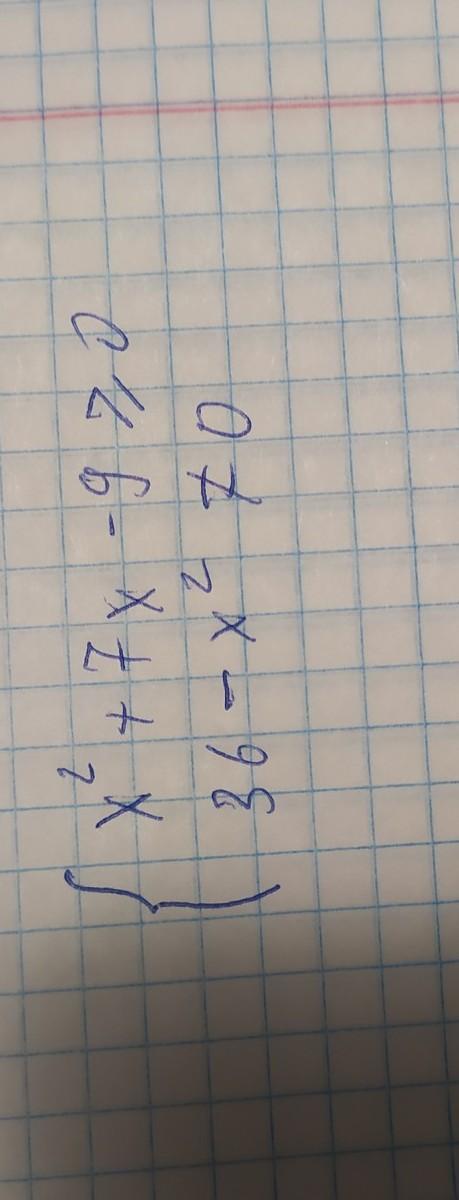
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: lera396
Предмет: Русский язык,
автор: fpuuv
Предмет: Русский язык,
автор: Miranda61442
Предмет: Биология,
автор: katyakuzmichevфа
Предмет: Алгебра,
автор: AdeleCookie