допоможіть алгебра 8 клас

Ответы
Ответ: для экономии места и времени в 3 номере сразу перевернула вторую дробь.
Объяснение:
Во вложении
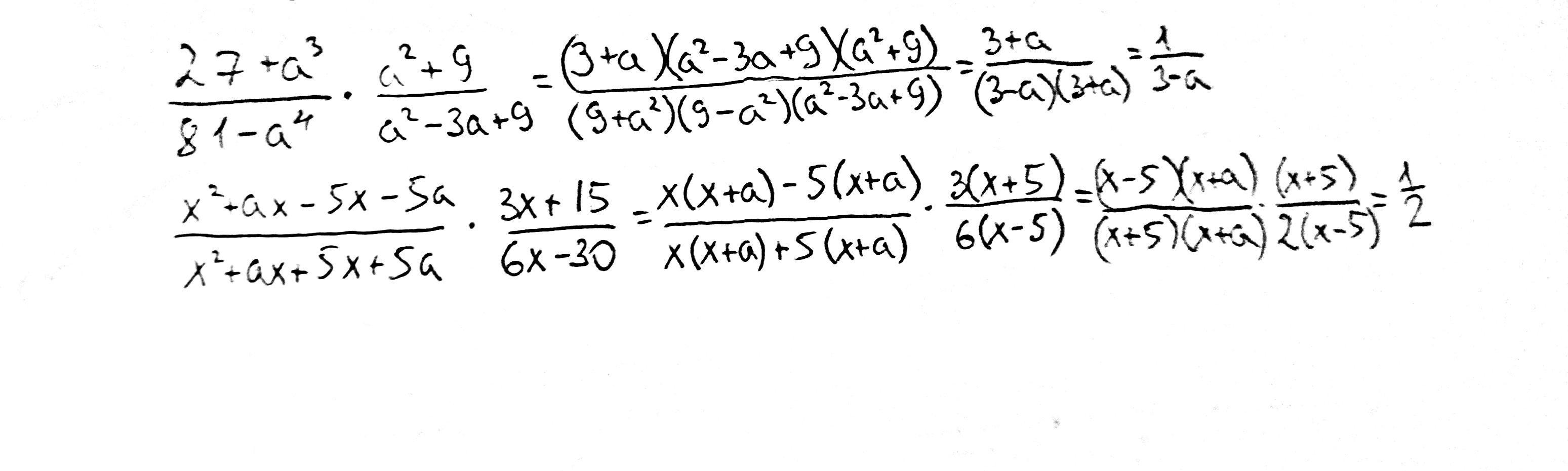
Ответ:
В решении.
Объяснение:
1) Выполнить деление:
(27 + а³)/(81 - а⁴) : (а²- 3а + 9)/(а² + 9)= -1/(а-3).
а) преобразовать левую часть выражения:
числитель (27 + а³) раскрыть по формуле суммы кубов:
(3³ + а³)= (3+а)(9-3а+а²);
знаменатель раскрыть как разность квадратов, а чтобы поменять местами члены скобки, т.к. это потребуется в дальнейшем решении, вынести за скобки знак минус:
(81 - а⁴) = - (а⁴ - 81) = -(а²-9)(а²+9);
Преобразованная левая часть:
[(3+а)(9-3а+а²)] / [-(а²-9)(а²+9)]=
= - [(3+а)(9-3а+а²)] / [(а²-9)(а²+9)];
б) Деление:
Чтобы разделить дробь на дробь, нужно числитель первой дроби умножить на знаменатель второй дроби, а знаменатель первой умножить на числитель второй дроби:
- [(3+а)(9-3а+а²)] / [(а²-9)(а²+9)] : [(а²-3а+9)/(а²+9)]=
= - [(3+а)(9-3а+а²) * (а²+9)] / [(а²-9)(а²+9) * (а²-3а+9)]=
сократить (разделить) (9-3а+а²) и (9-3а+а²) на (9-3а+а²), (а²+9) и (а²+9) на (а²+9):
= - (3+а)/(а²-9)=
в знаменателе раскрыть разность квадратов:
= -(3+а)/(а-3)(а+3)=
сократить (разделить) (3+а) и (а+3) на (а+3):
= -1/(а-3).
2) Вычислить значение выражения: при х=2,19; а= -8
(х²+ах-5х-5а)/(х²+ах+5х+5а) * (3х+15/(6х-30) = 1/2.
а) преобразовать левую часть выражения:
(х²+ах-5х-5а)/(х²+ах+5х+5а)=
= [(х²+ах)-(5х+5а)] / [(х²+ах)+(5х+5а)]=
=[x(x+a) - 5(x+a)] / [x(x+a) + 5(x+a)]=
=[(x+a)*(x-5)] / [(x+a)*(x+5)]=
сократить (разделить) (x+a) и (x+a) на (x+a):
=(х-5)/(х+5) - преобразованная левая часть.
б) преобразовать правую часть выражения:
(3х+15)/(6х-30) =
=[3(x+5)]/[6(x-5)] - преобразованная правая часть.
в) Умножение:
(х-5)/(х+5) * [3(x+5)]/[6(x-5)]=
Чтобы умножить дробь на дробь, нужно числитель первой дроби умножить на числитель второй, а знаменатель первой дроби умножить на знаменатель второй:
= [(x-5) * 3(x+5)] / [(x+5) * 6(x-5)]=
сократить (x-5) и (x-5) на (x-5), (x+5) и (x+5) на (x+5), 3 и 6 на 3:
=1/2.