как найти нод (180;360;240;80) и НОК (180;360;240;80) и сравните их.
Ответы
Ответ:
Наибольший общий делитель::
Разложим числа на простые множители и подчеркнем общие множители чисел:
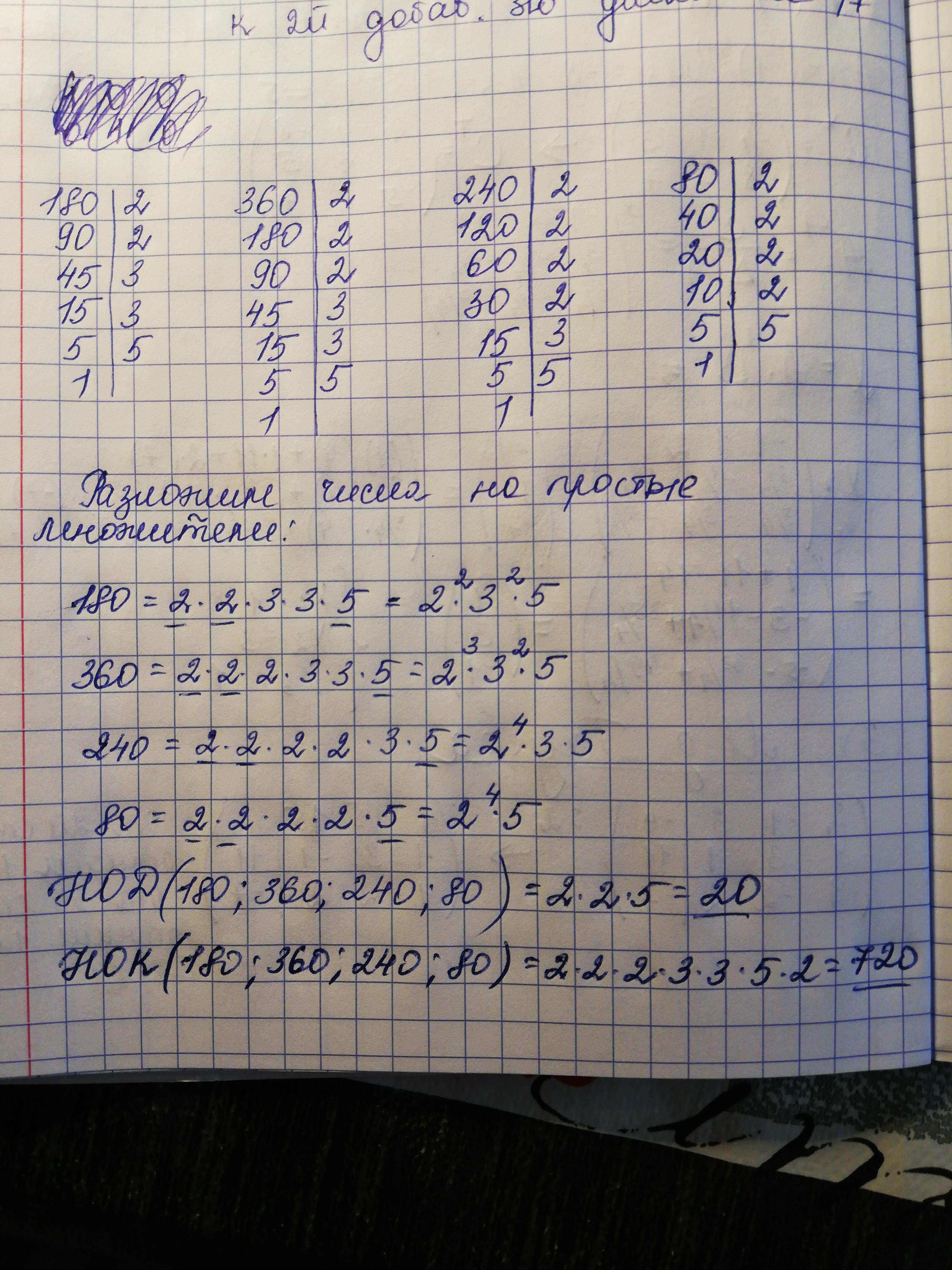
180 = 2 · 2 · 3 · 3 · 5
360 = 2 · 2 · 2 · 3 · 3 · 5
240 = 2 · 2 · 2 · 2 · 3 · 5
80 = 2 · 2 · 2 · 2 · 5
Общие множители чисел: 2; 2; 5
Чтобы найти НОД чисел, необходимо перемножить их общие множители:
НОД (180; 360; 240; 80) = 2 · 2 · 5 = 20
Наименьшее общее кратное::
Разложим числа на простые множители.
360 = 2 · 2 · 2 · 3 · 3 · 5
180 = 2 · 2 · 3 · 3 · 5
240 = 2 · 2 · 2 · 2 · 3 · 5
80 = 2 · 2 · 2 · 2 · 5
Чтобы определить НОК, необходимо недостающие множители (эти множители подчеркнуты) добавить к множителям большего числа и перемножить их:
НОК (180; 360; 240; 80) = 2 · 2 · 2 · 3 · 3 · 5 · 2 = 720
Ответ:
Наибольший общий делитель НОД (180; 360; 240; 80) = 20
Наименьшее общее кратное НОК (180; 360; 240; 80) = 720
вывод нок всегда нод
Пошаговое объяснение:
Відповідь:
НОК(180,360,240,80)=720
НОД(180,360,240,80)=20
Покрокове пояснення: