Question

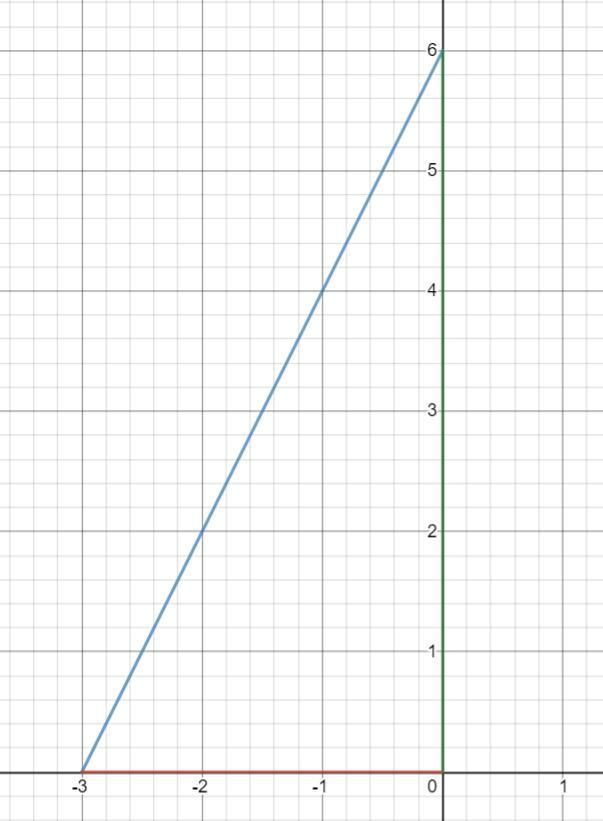
Який периметр трикутника, якщо він обмежений осями координат та прямою y=2x+6?​

Answer 1

Ответ:

$P=9+3\sqrt{5}$

Пошаговое объяснение:

Т.к. треугольник ограничен координатными осями, то это прямоугольный треугольник.

Катетами такого треугольника будут отрезки, отсекаемые графиком функции  $y=2x+6$ . Найдем длины этих катетов

Длина катета по оси OX:

$L_x = |(y-6):2| = |(0-6):2| = |-3| = 3$

Длина катета по оси OY:

$L_y = |2x+6| = |0+6| = 6$

Длину гипотенузы найдем из теоремы Пифагора:

$L=\sqrt{L_x^2+L_y^2} =\sqrt{3^2+6^2}=\sqrt{9+36} =\sqrt{45} =3\sqrt{5}$

И тогда периметр равен:

$P=L_x+L_y+L=3+6+3\sqrt{5} =9+3\sqrt{5}$