Предмет: Математика,
автор: oonostosyan
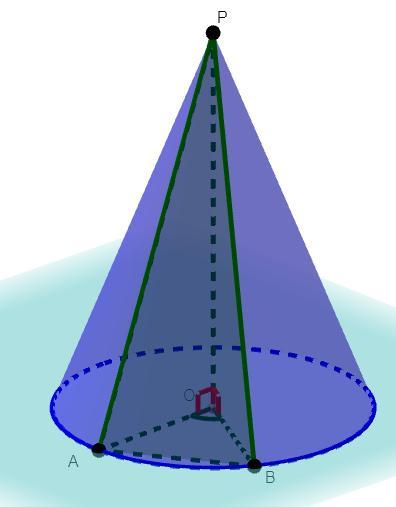
Высота прямого кругового конуса РО = 7, радиус основания ОА = ОВ = 6, угол АОВ равен 30°.
Найдите объем треугольной пирамиды РОАВ.
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Дано: РО = 7, PO - высота прямого кругового конуса, ОА = ОВ = 6,
∠AOB = 30° , O - цент окружности
Найти: - ?
Решение: Рассмотрим треугольник ΔAOB. По формуле площади треугольника: .
По формуле объема пирамиды:
кубических единиц.
Приложения:
Похожие вопросы
Предмет: Другие предметы,
автор: Nicto55555
Предмет: Русский язык,
автор: nastea2002
Предмет: Английский язык,
автор: TheWalkingead7120
Предмет: Алгебра,
автор: RiZeReS
Предмет: Математика,
автор: maks200906