Question

.........................................

Answer 1

1) В ΔАВС , точка Е -середина ВС, ∠1=∠2.  Доказать АD=DB

Объяснение:

Т.к ∠1=∠2 и они накрест лежащие, то АС║DE , секущая АВ.

Угол ∠АВС  пересекает две параллельные прямые  и ВЕ=ЕС ⇒ по т. Фалеса   АD=DB.

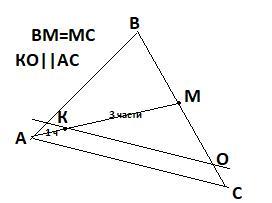
2) На медиане АМ  ΔАВС взята точка К , причем АК/КМ=1/3.Найдите отношение , в котором прямая, проходящая через точку К параллельно АС, делит сторону ВС .

Объяснение:

Пусть КО║АС , О∈ВС . Нужно найти  $\frac{BO}{OC}$ .

Угол ∠АMC  пересекает две параллельные прямые AC и КО  ⇒

по т. Фалеса  (более общая  т. о пропорциональных отрезках  )  

$\frac{KM}{AK} =\frac{MO}{OC}$  ,  $\frac{3}{1} =\frac{MO}{OC}$ .

$\frac{BO}{OC}=\frac{BM+MO}{OC}=\frac{MC+MO}{OC}=\frac{MO+OC+MO}{OC}=\frac{OC+2MO}{OC}=1+2*3=7$

$\frac{BO}{OC}=\frac{7}{1}$  .