Предмет: Геометрия,
автор: Екатерина525
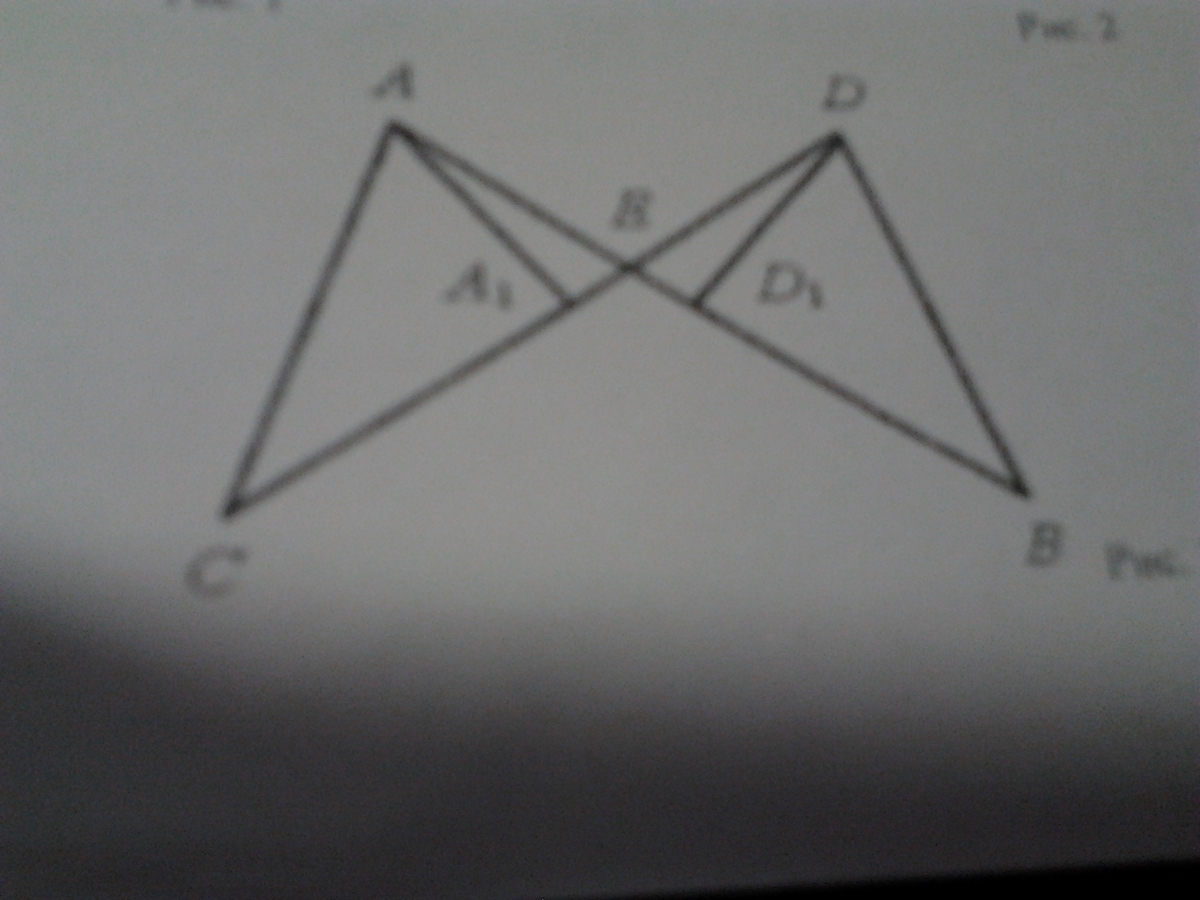
на рисунке 3 прямые AB и CD пересекаются в точке Е , СЕ=ВЕ ,угол С= углу В; АА1 и DD1-биссектрисы треугольников АСЕ и DBE. Докажите, что АА1=DD1
Приложения:
Ответы
Автор ответа:
0
СЕ = DB по условию,
∠АСЕ = ∠DBE по условию,
∠АЕС = ∠DEB как вертикальные, ⇒
ΔАЕС = ΔDEB по стороне и двум прилежащим к ней углам.
Значит, АЕ = DE и ∠САЕ = ∠BDE.
Тогда и ∠ЕАА₁ = ∠EDD₁ как половины равных углов,
∠АЕС = ∠DEB как вертикальные,
Следовательно, ΔЕАА₁ = ΔEDD₁ по стороне и двум прилежащим к ней углам.
Значит, АА₁ = DD₁.
∠АСЕ = ∠DBE по условию,
∠АЕС = ∠DEB как вертикальные, ⇒
ΔАЕС = ΔDEB по стороне и двум прилежащим к ней углам.
Значит, АЕ = DE и ∠САЕ = ∠BDE.
Тогда и ∠ЕАА₁ = ∠EDD₁ как половины равных углов,
∠АЕС = ∠DEB как вертикальные,
Следовательно, ΔЕАА₁ = ΔEDD₁ по стороне и двум прилежащим к ней углам.
Значит, АА₁ = DD₁.
Похожие вопросы
Предмет: Литература,
автор: bebko05
Предмет: Другие предметы,
автор: juliakozina10
Предмет: Алгебра,
автор: sv17122
Предмет: Алгебра,
автор: IrIsKaaaaa
Предмет: География,
автор: razfankos