Предмет: Геометрия,
автор: Chinderella0
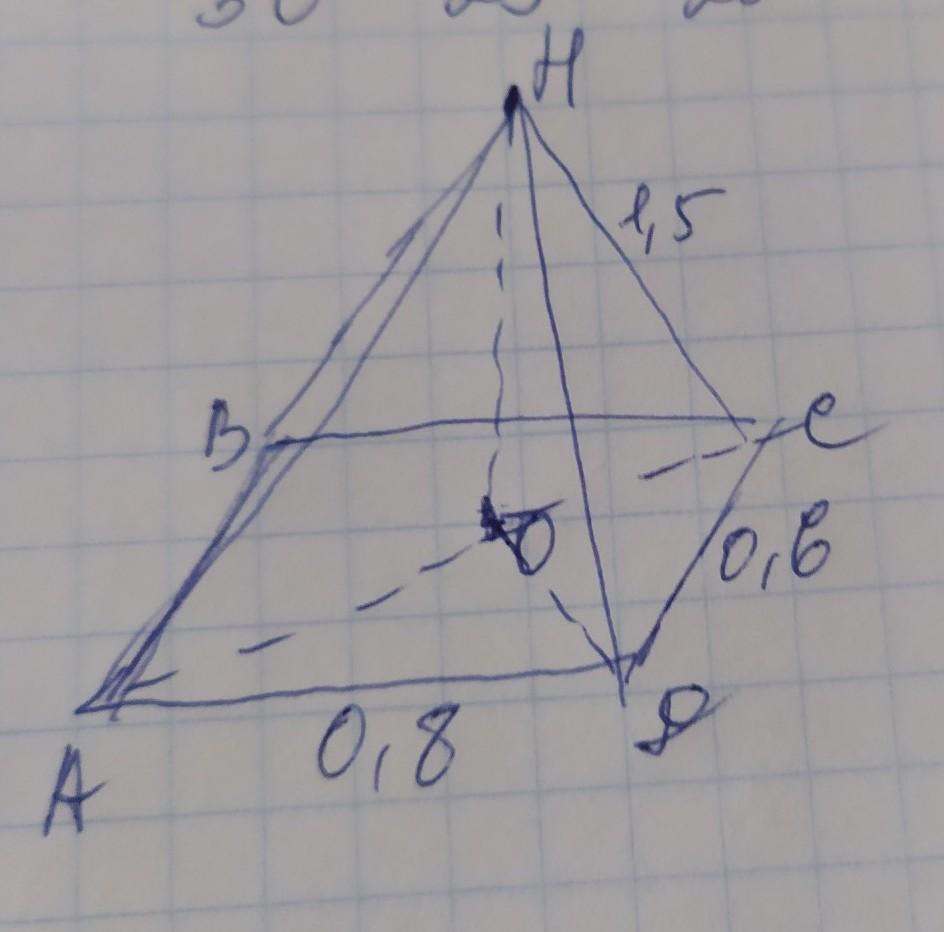
Основание пирамиды представляет собой прямоугольник со сторонами 0,6 дм и 0,8 дм. Каждая сторона пирамиды составляет 1,5 дм. Найдите его высоту.
Iife20:
сторона пирамиды - это её ребро?
да.
спасибо))
тебе спасибо за решение
рада была помочь))
Ответы
Автор ответа:
1
Ответ:
НО=√2дм
Объяснение:
обозначим вершины основания пирамиды А В С Д, точку пересечения диагоналей основания АС и ВД - О, а верх пирамиды Н, и нужно будет найти НО. Диагонали прямоугльника Так как диагональ прямоугльника делит его на 2 равных прямоугольных треугольника, в которых стороны основания являются катетами а диагональ - гипотенуза. Найдём диагональ АС по теореме Пифагора:
АС²=АД²+СД²=0,8²+0,6²=0,64+0,36=1; АС=√1=1дм
При пересечении диагонали основания делятся пополам, поэтому АО=СО=1÷2=0,5дм
Эта половина диагонали основания вместе с ребром и высотой пирамиды образуют прямоугольный треугольник с катетами НО и СО и гипотенузой НС. Найдём высоту НО по теореме Пифагора:
НО²=НС²–СО²=1,5²–0,5²=2,25–0,25=2; НО=√2дм
Приложения:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: ansanna627
Предмет: Русский язык,
автор: аделя22
Предмет: Русский язык,
автор: smirnovadar20
Предмет: Математика,
автор: Sop4