Предмет: Алгебра,
автор: alexx1221gg
Решите показательное неравенство и показательную систему уравнений, пожалуйста
Приложения:
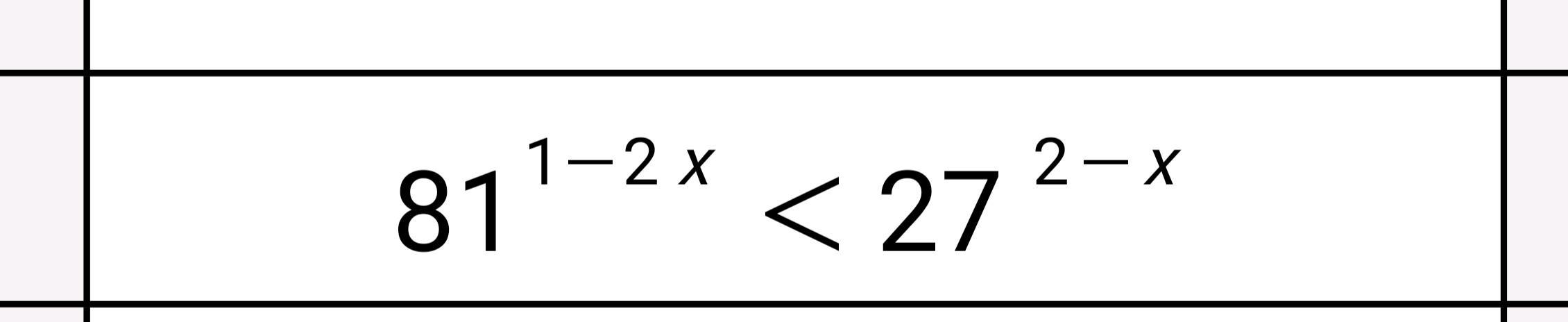
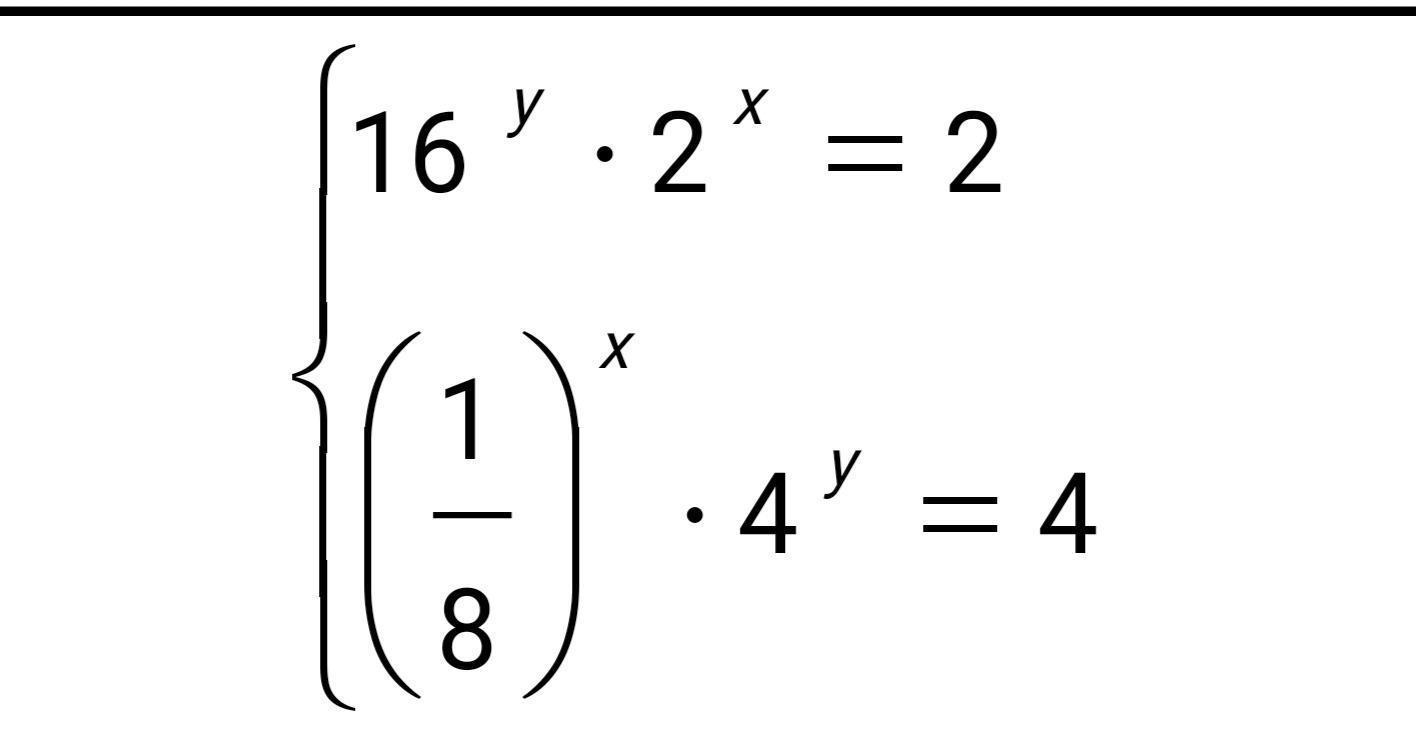
Ответы
Автор ответа:
1
Ответ:
решение на фотографиях
Приложения:
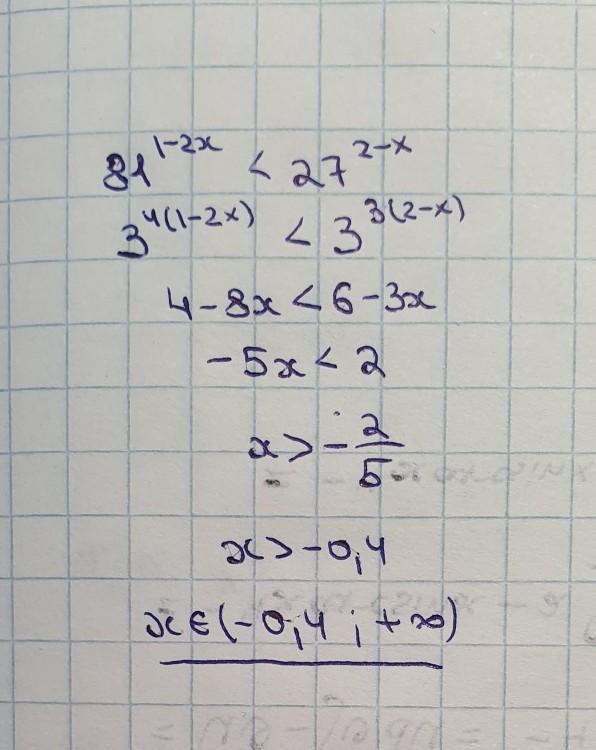

Автор ответа:
1
Объяснение:
Ответ: x∈(-0,4;+∞).
Суммируем эти уравнения:
Ответ: (-3/7;5/14).
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Английский язык,
автор: AlinaAubakirova
Предмет: Русский язык,
автор: Vikylj11
Предмет: Математика,
автор: АЯН988
Предмет: История,
автор: vasiliysmirnov2