Предмет: Алгебра,
автор: alexx1221gg
Решите показательные уравнения, пожалуйста
Приложения:
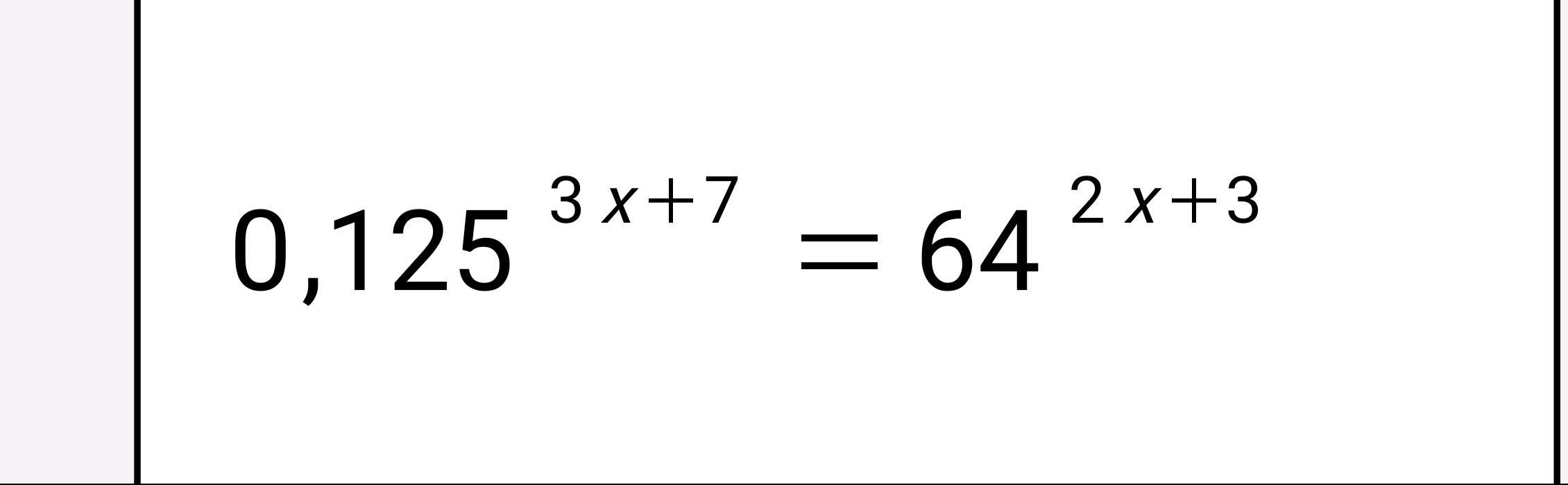
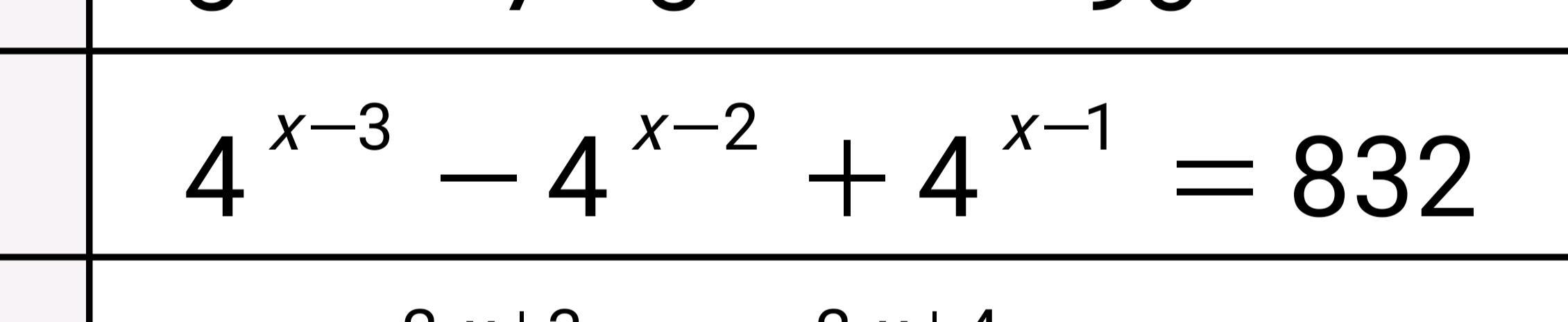
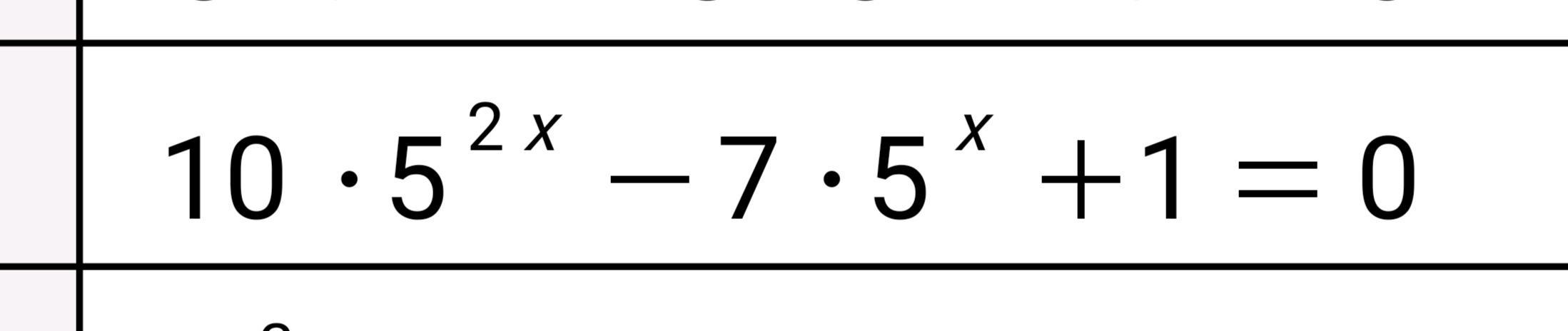
Ответы
Автор ответа:
1
Ответ:
Надеюсь всё хорошо видно)
Объяснение:
Приложения:

LFP:
1. можно было остановиться на основании 8...
8^(-3х-7) = 8^(4х+6) ---> 7х=-13
2. в показателе степени: х+1-х+3 = 4)) а, вы сам пример неверно переписали...
Автор ответа:
1
Ответ:
1)
2) 6
3) x₁=-㏒₅2; x₂=-1
Объяснение:
1)
2)
3)
Пусть тогда:
Подставляем значения y:
x₁=-㏒₅2; x₂=-1
Похожие вопросы
Предмет: Русский язык,
автор: vikahka116
Предмет: Русский язык,
автор: yalybom
Предмет: Русский язык,
автор: ZZZZ34
Предмет: Математика,
автор: EGAHOCKEY
Предмет: Математика,
автор: ютубер456